Vị trí tương đối của đường thẳng với đường tròn

Do đường tròn tiếp xúc với trục $Oy$ nên $R = d\left( {I,Oy} \right) = \left| {{x_I}} \right|$.

Phương trình trục $Oy$ là $x = 0$.

Đáp án A sai vì: Tâm $I\left( {0;5} \right)$ và bán kính $R = \sqrt {24} $. Ta có $d\left( {I,Oy} \right) = \left| {{x_I}} \right| \ne R$.

Đáp án B sai vì: Tâm $I\left( { - 3; - \dfrac{5}{2}} \right)$ và bán kính $R = \dfrac{{\sqrt {65} }}{2}$. Ta có $d\left( {I,Oy} \right) = \left| {{x_I}} \right| \ne R$.

Đáp án C đúng vì: Tâm $I\left( {1;0} \right)$ và bán kính $R = 1$. Ta có $d\left( {I,Oy} \right) = \left| {{x_I}} \right| = R$.

Đáp án D sai vì: Tâm $I\left( {0;0} \right)$ và bán kính $R = \sqrt 5 $. Ta có $d\left( {I,Oy} \right) = \left| {{x_I}} \right| \ne R$.

Do đường tròn tiếp xúc với trục $Ox$ nên $R = d\left( {I,Ox} \right) = \left| {{y_I}} \right|$.

Phương trình trục $Ox$ là $y = 0$.

Đáp án A sai vì: Tâm $I\left( {1;5} \right)$ và bán kính $R = \sqrt {26} $. Ta có $d\left( {I,Ox} \right) = \left| {{y_I}} \right| \ne R$.

Đáp án B đúng vì: Tâm $I\left( { - 3; - \dfrac{5}{2}} \right)$ và bán kính $R = \dfrac{5}{2}$. Ta có $d\left( {I,Ox} \right) = \left| {{y_I}} \right| = R$.

Đáp án C sai vì: Tâm $I\left( {0;5} \right)$ và bán kính $R = \sqrt {24} $. Ta có $d\left( {I,Ox} \right) = \left| {{y_I}} \right| \ne R$.

Đáp án D sai vì: Tâm $I\left( {0;0} \right)$ và bán kính $R = \sqrt 5 $. Ta có $d\left( {I,Ox} \right) = \left| {{y_I}} \right| \ne R$.

Ta có:${x^2} + {y^2} - 4x - 2y + 1 = 0 \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 4$ có tâm $I\left( {2;{\rm{ }}1} \right)$, bán kính $R = 2.$

Vì $d\left( {I,Oy} \right) = 2,$ $d\left( {I,Ox} \right) = 1,$$d\left( {I,{\Delta _1}} \right) = \dfrac{9}{{2\sqrt 5 }},$ $d\left( {I,{\Delta _2}} \right) = \dfrac{1}{{\sqrt 5 }}$ nên A đúng.

Dễ thấy \(A \in \Delta \) nên tâm I của đường tròn nằm trên đường thẳng qua A vuông góc với \(\Delta \) là

\(\Delta ':4x + 3y + 5 = 0\)\( \to I = \Delta ' \cap d:\left\{ \begin{array}{l}4x + 3y + 5 = 0\\x + 3y + 8 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 3\end{array} \right. \to \left\{ \begin{array}{l}I\left( {1; - 3} \right)\\R = IA = 5\end{array} \right.\)

      Vậy phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 25.\)

\((C):{x^2} + {y^2} - 4x - 4y - 8 = 0\) có tâm \(I\left( {2;2} \right),\,\,R = \sqrt {{2^2} + {2^2} + 8}  = 4\).

Tiếp tuyến song song với đường thẳng \((d):x - y - 1 = 0\) nên phương trình tiếp tuyến có dạng \(x - y + c = 0\) với \(c \ne  - 1\) (d’)

Vì d’ là tiếp tuyến của đường tròn có tâm \(I\left( {2;2} \right)\) và \(R = 4\) nên ta có

\(d\left( {I;d'} \right) = R \Leftrightarrow \dfrac{{\left| {2 - 2 + c} \right|}}{{\sqrt 2 }} = 4 \Leftrightarrow |c| = 4\sqrt 2  \Leftrightarrow c =  \pm 4\sqrt 2 \)   

Xét hệ:$\;\left\{ {\begin{array}{*{20}{c}}{{x^2} + {y^2} - 2 = 0}\\{{x^2} + {y^2} - 2x = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{{y^2} = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{\left[ {\begin{array}{*{20}{c}}{y = 1}\\{y =  - 1}\end{array}} \right.}\end{array}} \right.$

Vậy có hai giao điểm là:$\left( {1;{\rm{ }} - 1} \right)$và $\left( {1;{\rm{ }}1} \right)$.

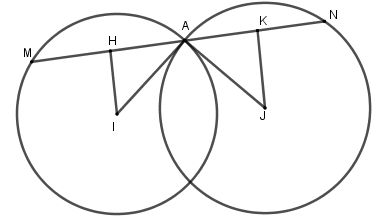
- Từ giả thiết : \(\left( {{C_1}} \right):\;I = \left( {0;0} \right),R = \sqrt {13} .\left( {{C_2}} \right);J\left( {6;0} \right),R' = 5\)

- Gọi đường thẳng \(d\) qua \(A\left( {2;3} \right)\) có véc tơ chỉ phương \(\overrightarrow n  = \left( {a;b} \right)\) \( \Rightarrow d:a\left( {x - 2} \right) + b\left( {y - 3} \right) = 0\) \( \Leftrightarrow ax + by - 2a - 3b = 0\).

Dễ thấy \(AH = AK\) (vì \(AM = AN\)) nên $I{A^2} - I{H^2} = J{A^2} - J{K^2}$ \( \Leftrightarrow 13 - {d^2}\left( {I,d} \right) = 25 - {d^2}\left( {J,d} \right)\) \( \Leftrightarrow {d^2}\left( {J,d} \right) - {d^2}\left( {I,d} \right) = 12\).

Mà \(d\left( {I,d} \right) = \dfrac{{\left| { - 2a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) và \(d\left( {J,d} \right) = \dfrac{{\left| {4a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) nên:

\(\dfrac{{16{a^2} - 24ab + 9{b^2}}}{{{a^2} + {b^2}}} - \dfrac{{4{a^2} + 12ab + 9{b^2}}}{{{a^2} + {b^2}}} = 12\) \( \Leftrightarrow 12{a^2} - 36ab = 12{a^2} + 12{b^2}\)

\( \Leftrightarrow 12{b^2} =  - 36ab \Leftrightarrow \left[ \begin{array}{l}b = 0\\b =  - 3a\end{array} \right.\).

Nếu \(b = 0\) thì chọn \(a = 1\) ta được phương trình \(x - 2 = 0\).

Nếu \(b =  - 3a\) thì chọn \(a = 1\) ta được \(b =  - 3\), ta được phương trình \(x - 3y + 7 = 0\).

Vậy có 2 đường thẳng: \({d_1}:x - 2 = 0\) và \({d_2}:x - 3y + 7 = 0\).

- \(\left( C \right)\) có \(I\left( { - 2\sqrt 3 ;0} \right)\), \(R = 4\). Gọi \(J\) là tâm đường tròn cần tìm: \(J(a;b)\)\( \Rightarrow \left( {C'} \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = 4\)

-Do \(\left( C \right)\) và \(\left( {C'} \right)\) tiếp xúc ngoài với nhau cho nên khoảng cách \(IJ = R + R'\)\( \Rightarrow \sqrt {{{\left( {a + 2\sqrt 3 } \right)}^2} + {b^2}}  = 4 + 2 = 6\) \( \Leftrightarrow {a^2} + 4\sqrt 3 a + {b^2} = 28\)

- Vì \(A\left( {0;2} \right)\) là tiếp điểm cho nên : \({\left( {0 - a} \right)^2} + {\left( {2 - b} \right)^2} = 4\left( 2 \right)\)

- Do đó ta có hệ : \(\left\{ \begin{array}{l}{\left( {a + 2\sqrt 3 } \right)^2} + {b^2} = 36\\{a^2} + {\left( {2 - b} \right)^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} + 4\sqrt 3 a + {b^2} = 24\\{a^2} - 4b + {b^2} = 0\end{array} \right.\)

- Giải hệ tìm được: \(b = 3\) và \(a = \sqrt 3  \Rightarrow \left( {C'} \right):{\left( {x - \sqrt 3 } \right)^2} + {\left( {y - 3} \right)^2} = 4\).

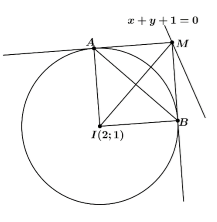
- \(M\) thuộc \(d\) suy ra \(M(t; - 1 - t)\).

Nếu 2 tiếp tuyến vuông góc với nhau thì \(MAIB\) là hình vuông (\(A\),\(B\) là 2 tiếp điểm). Do đó \(AB = MI = IA\sqrt 2  = R\sqrt 2  = \sqrt 6 .\sqrt 2  = 2\sqrt 3 \)

- Ta có : \(MI = \sqrt {{{\left( {2 - t} \right)}^2} + {{\left( {2 + t} \right)}^2}}  = \sqrt {2{t^2} + 8}  = 2\sqrt 3 \)

- Do đó : \(2{t^2} + 8 = 12\)\( \Leftrightarrow {t^2} = 2\)\( \Leftrightarrow \left[ \begin{array}{l}t =  - \sqrt 2  \to {M_1}\left( { - \sqrt 2 ;\sqrt 2  - 1} \right)\\t = \sqrt 2  \to {M_2}\left( {\sqrt 2 ; - \sqrt 2  - 1} \right)\end{array} \right.\)

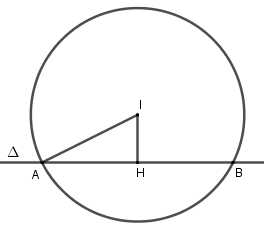
Gọi \(\Delta \) là đường thẳng song song với \(d\) nên \(\Delta \) có dạng \(3x + 4y + c = 0\left( {c \ne  - 2} \right)\)

\(\Delta \) cắt \(\left( C \right)\) tại \(A,B\) nên \(AB = 6\).

Gọi \(H\) là trung điểm của \(AB\) thì \(AH = \dfrac{{AB}}{2} = \dfrac{6}{2} = 3\)

Tam giác \(IAH\) vuông tại \(H\) nên \(IH = \sqrt {I{A^2} - A{H^2}}  = \sqrt {{5^2} - {3^2}}  = 4\)

Mà \(IH = d\left( {I,\Delta } \right) \Rightarrow 4 = \dfrac{{\left| {3.\left( { - 1} \right) + 4.4 + c} \right|}}{{\sqrt {{3^2} + {4^2}} }}\)

\(\begin{array}{l} \Leftrightarrow 4 = \dfrac{{\left| {13 + c} \right|}}{5} \Leftrightarrow \left| {13 + c} \right| = 20\\ \Leftrightarrow \left[ \begin{array}{l}13 + c = 20\\13 + c =  - 20\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}c = 7\\c =  - 33\end{array} \right.\left( {TM} \right)\end{array}\)

Vậy có hai đường thẳng cần tìm là: \({\Delta _1}:3x + 4y + 7 = 0\) và \({\Delta _2}:3x + 4y - 33= 0\)

Gọi \(d\) là đường thẳng qua \(M\) có véc tơ chỉ phương \(\overrightarrow u  = \left( {a;b} \right) \Rightarrow d:\left\{ \begin{array}{l}x = 1 + at\\y = bt\end{array} \right.\)

- Đường tròn \(\left( {{C_1}} \right):{I_1}\left( {1;1} \right),{R_1} = 1\;.\;\left( {{C_2}} \right):\;{I_2}\left( { - 2;0} \right),{R_2} = 3\) , suy ra :

\(\left( {{C_1}} \right):\;{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1,\;\left( {{C_2}} \right):\;{\left( {x + 2} \right)^2} + {y^2} = 9\)

- Nếu d cắt  \(\left( {{C_1}} \right)\) tại \(A\): \( \Rightarrow \left( {{a^2} + {b^2}} \right){t^2} - 2bt = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0 \to M\\t = \dfrac{{2b}}{{{a^2} + {b^2}}}\end{array} \right. \Rightarrow A\left( {1 + \dfrac{{2ab}}{{{a^2} + {b^2}}};\dfrac{{2{b^2}}}{{{a^2} + {b^2}}}} \right)\)

- Nếu d cắt \(\left( {{C_2}} \right)\) tại \(B\): \( \Rightarrow \left( {{a^2} + {b^2}} \right){t^2} + 6at = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0 \to M\\t =  - \dfrac{{6a}}{{{a^2} + {b^2}}}\end{array} \right. \Leftrightarrow B\left( {1 - \dfrac{{6{a^2}}}{{{a^2} + {b^2}}}; - \dfrac{{6ab}}{{{a^2} + {b^2}}}} \right)\)

- Theo giả thiết: \(MA = 2MB\)\( \Leftrightarrow M{A^2} = 4M{B^2}\left( * \right)\)

- Ta có : \({\left( {\dfrac{{2ab}}{{{a^2} + {b^2}}}} \right)^2} + {\left( {\dfrac{{2{b^2}}}{{{a^2} + {b^2}}}} \right)^2} = 4\left[ {{{\left( {\dfrac{{6{a^2}}}{{{a^2} + {b^2}}}} \right)}^2} + {{\left( {\dfrac{{6ab}}{{{a^2} + {b^2}}}} \right)}^2}} \right]\)

\( \Leftrightarrow \dfrac{{4{b^2}}}{{{a^2} + {b^2}}} = 4.\dfrac{{36{a^2}}}{{{a^2} + {b^2}}} \Leftrightarrow {b^2} = 36{a^2}\)\( \Leftrightarrow \left[ \begin{array}{l}b =  - 6a \to d:6x + y - 6 = 0\\b = 6a \to d:6x - y - 6 = 0\end{array} \right.\)

\(\Delta ABC\) cân tại \(A\); tâm \(I\) của \(\left( C \right)\) thuộc \(Oy\)$ \Rightarrow I\left( {0;{y_0}} \right)$, $\overrightarrow {IB}  = \left( {b; - {y_0}} \right),\;\overrightarrow {AB}  = \left( {b; - a} \right)$.

Do $\overrightarrow {IB} .\overrightarrow {AB}  = 0 \Rightarrow {b^2} + a{y_0} = 0 \Rightarrow {y_0} =  - \dfrac{{{b^2}}}{a}$.

Mặc khác  ${R^2} = I{B^2} = {b^2} + y_0^2 = {b^2} + \dfrac{{{b^4}}}{{{a^2}}}$ .

Vậy phương trình của \(\left( C \right)\) là ${x^2} + {\left( {y + \dfrac{{{b^2}}}{a}} \right)^2} = {b^2} + \dfrac{{{b^4}}}{{{a^2}}}$.

Đường tròn \(\left( C \right)\) có tâm \(I\left( {4, - 3} \right)\), bán kính \(R = 2\)

Tọa độ của \(I(4, - 3)\) thỏa phương trình \(d:x + y - 1 = 0\). Vậy \(I \in d\).

Vậy \(AI\) là một đường chéo của hình vuông ngoại tiếp đường tròn, có bán kính \(R = 2\), \(x = 2\) và \(x = 6\) là \(2\) tiếp tuyến của \(\left( C \right)\)  nên

Hoặc là \(A\) là giao điểm các đường \(d\) và \(x = 2 \Rightarrow A\left( {2, - 1} \right)\)

Hoặc là \(A\) là giao điểm các đường  \((d)\) và \(x = 6 \Rightarrow A\left( {6, - 5} \right)\).

\(\left( C \right):{\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 5\) có tâm \(I\left( {3; - 1} \right)\) và bán kính \(R = \sqrt 5 .\)

\(MI = \sqrt {{{\left( {3 - 4} \right)}^2} + {{\left( { - 1 - 1} \right)}^2}}  = \sqrt 5 \) nên \(M \in \left( C \right).\)

\( \Rightarrow \overrightarrow {MI}  = \left( { - 1; - 2} \right)\) là một vectơ pháp tuyến của tiếp tuyến tại \(M\) với đường tròn \(\left( C \right)\).

Vậy tiếp tuyến tại \(M\) của đường tròn \(\left( C \right)\) có phương trình là:

\( - \left( {x - 4} \right) - 2\left( {y - 1} \right) = 0 \Leftrightarrow x + 2y - 6 = 0.\)

Đường tròn tâm \(I\left( {1;3} \right)\) tiếp xúc với đường thẳng \(\Delta :3x + 4y = 0\)

\( \Leftrightarrow R = d\left( {I,\Delta } \right) = \dfrac{{\left| {3.1 + 4.3} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \dfrac{{15}}{5} = 3\)

Gọi \(\Delta \) là tiếp tuyến cần tìm.

Đường tròn \(\left( C \right)\) có tâm \(O\left( {0;0} \right)\) \( \Rightarrow \Delta  \bot OM\)

\( \Rightarrow \overrightarrow {OM}  = \left( {1;1} \right)\) là một VTPT của \(\Delta \)

\( \Rightarrow \) Phương trình \(\Delta :\,\,1\left( {x - 1} \right) + 1\left( {y - 1} \right) = 0 \Leftrightarrow x + y - 2 = 0\)

Đường tròn \(\left( C \right)\) có tâm \(I\left( {0;0} \right)\)

Gọi \(\Delta \) là tiếp tuyến cần tìm

\( \Rightarrow \overrightarrow {IA}  = \left( {3;4} \right)\) là một VTPT của \(\Delta \)

\( \Rightarrow \Delta :3\left( {x - 3} \right) + 4\left( {y - 4} \right) = 0 \Leftrightarrow 3x + 4y - 25 = 0\)

Đường tròn \(\left( C \right):{x^2} + {y^2} - 8x + 12 = 0\) có tâm \(I\left( {4;0} \right)\) và bán kính \(R = 2\).

Gọi \(\left( {C'} \right)\) là đường tròn tâm \(M\) bán kính \(MA\) thì \(A,B\) là các giao điểm của hai đường tròn \(\left( C \right)\) và \(\left( {C'} \right)\).

Điểm \(M \in Oy \Rightarrow M\left( {0;m} \right)\). Khi đó \(MI = \sqrt {{{\left( {4 - 0} \right)}^2} + {{\left( {0 - m} \right)}^2}}  = \sqrt {{m^2} + 16} \).

Tam giác \(MIA\) vuông tại \(A\) \( \Leftrightarrow M{A^2} + I{A^2} = M{I^2}\) \( \Leftrightarrow M{A^2} + 4 = {m^2} + 16\) \( \Leftrightarrow M{A^2} = {m^2} + 12\).

Đường tròn \(\left( {C'} \right)\) tâm \(M\left( {0;m} \right)\) bán kính \(MA = \sqrt {{m^2} + 12} \) có phương trình:

\({\left( {x - 0} \right)^2} + {\left( {y - m} \right)^2} = {m^2} + 12\) \( \Leftrightarrow {x^2} + {y^2} - 2my - 12 = 0\).

Do \(\left\{ {A,B} \right\} = \left( C \right) \cap \left( {C'} \right)\) nên tọa độ của \(A,B\) thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}{x^2} + {y^2} - 8x + 12 = 0\,\,\,\left( 1 \right)\\{x^2} + {y^2} - 2my - 12 = 0\,\,\left( 2 \right)\end{array} \right.\).

Lấy \(\left( 1 \right) - \left( 2 \right)\) ta được: \( - 8x + 2my + 24 = 0\) hay phương trình \(AB: - 8x + 2my + 24 = 0\).

Do \(K\left( {4;1} \right) \in AB\) nên \( - 8.4 + 2m.1 + 24 = 0\) \( \Leftrightarrow m = 4\).

Vậy \(M\left( {0;4} \right)\) hay \(a = 0,b = 4\) \( \Rightarrow T = {0^2} + {4^2} = 16\).

Đường tròn \(\left( C \right)\) có tâm \(O\left( {1; - 2} \right)\)

Gọi \(\Delta \) là tiếp tuyến của \(\left( C \right)\) tại  A\( \Rightarrow OA \bot \Delta \)

Ta có: \(\overrightarrow {OA}  = \left( { - 3;4} \right)\) là một VTPT của \(\Delta \)

 Phương trình \(\Delta \): \( - 3\left( {x + 2} \right) + 4\left( {y - 2} \right) = 0 \Leftrightarrow 3x - 4y + 14 = 0.\) 

Đường tròn \(\left( C \right)\) có tâm \(I\left( {0;0} \right)\) bán kính \(R = \sqrt {0 + 0 + 16}  = 4\)

Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( C \right)\)\( \Leftrightarrow d\left( {I;\Delta } \right) = R\)

\( \Leftrightarrow \dfrac{{\left| {m - 1} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 4 \Leftrightarrow \left| {m - 1} \right| = 20 \Leftrightarrow \left[ \begin{array}{l}m - 1 = 20\\m - 1 =  - 20\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = 21\\m =  - 19\end{array} \right.\)