Câu hỏi:
2 năm trước
Trong mặt phẳng với hệ toạ độ \(Oxy\), cho đường tròn \(\left( C \right):{x^2} + {y^2} + 2x - 8y - 8 = 0\). Viết phương trình đường thẳng song song với đường thẳng \(d:3x + 4y - 2 = 0\) và cắt đường tròn theo một dây cung có độ dài bằng \(6\).
Trả lời bởi giáo viên
Đáp án đúng: c
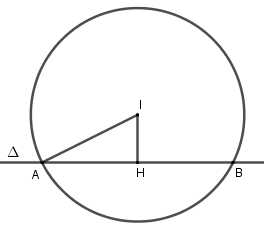
Gọi \(\Delta \) là đường thẳng song song với \(d\) nên \(\Delta \) có dạng \(3x + 4y + c = 0\left( {c \ne - 2} \right)\)
\(\Delta \) cắt \(\left( C \right)\) tại \(A,B\) nên \(AB = 6\).
Gọi \(H\) là trung điểm của \(AB\) thì \(AH = \dfrac{{AB}}{2} = \dfrac{6}{2} = 3\)
Tam giác \(IAH\) vuông tại \(H\) nên \(IH = \sqrt {I{A^2} - A{H^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Mà \(IH = d\left( {I,\Delta } \right) \Rightarrow 4 = \dfrac{{\left| {3.\left( { - 1} \right) + 4.4 + c} \right|}}{{\sqrt {{3^2} + {4^2}} }}\)
\(\begin{array}{l} \Leftrightarrow 4 = \dfrac{{\left| {13 + c} \right|}}{5} \Leftrightarrow \left| {13 + c} \right| = 20\\ \Leftrightarrow \left[ \begin{array}{l}13 + c = 20\\13 + c = - 20\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}c = 7\\c = - 33\end{array} \right.\left( {TM} \right)\end{array}\)
Vậy có hai đường thẳng cần tìm là: \({\Delta _1}:3x + 4y + 7 = 0\) và \({\Delta _2}:3x + 4y - 33= 0\)
Hướng dẫn giải:
- Viết dạng của đường thẳng \(\Delta\) sử dụng điều kiện \(\Delta//d\).
- Viết công thức tính \(d\left( {I,\Delta} \right)\) và sử dụng công thức \({d^2} + \dfrac{{A{B^2}}}{4} = {R^2}\).
Câu hỏi khác
- Bài tập một số khái niệm phương trình đường thẳng toán 10 có lời giải
- Bài tập vị trí tương đối của đường thẳng với đường tròn toán 10 có lời giải
- Bài tập một số bài toán viết phương trình đường thẳng toán 10 có lời giải
- Bài tập phương trình đường tròn toán 10 có lời giải
- Bài tập khoảng cách và góc toán 10 có lời giải
