Câu hỏi:
2 năm trước
Trong mặt phẳng với hệ tọa độ \(Oxy\). Cho đường tròn $\left( C \right):{x^2} + {y^2} - 4x - 2y - 1\,\, = \,\,0$và đường thẳng $d:x + y + 1\,\, = \,\,0$. Tìm những điểm \(M\) thuộc đường thẳng \(d\) sao cho từ điểm \(M\) kẻ được đến \(\left( C \right)\) hai tiếp tuyến hợp với nhau góc \({90^0}\).
Trả lời bởi giáo viên
Đáp án đúng: a
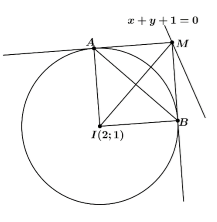
- \(M\) thuộc \(d\) suy ra \(M(t; - 1 - t)\).
Nếu 2 tiếp tuyến vuông góc với nhau thì \(MAIB\) là hình vuông (\(A\),\(B\) là 2 tiếp điểm). Do đó \(AB = MI = IA\sqrt 2 = R\sqrt 2 = \sqrt 6 .\sqrt 2 = 2\sqrt 3 \)
- Ta có : \(MI = \sqrt {{{\left( {2 - t} \right)}^2} + {{\left( {2 + t} \right)}^2}} = \sqrt {2{t^2} + 8} = 2\sqrt 3 \)
- Do đó : \(2{t^2} + 8 = 12\)\( \Leftrightarrow {t^2} = 2\)\( \Leftrightarrow \left[ \begin{array}{l}t = - \sqrt 2 \to {M_1}\left( { - \sqrt 2 ;\sqrt 2 - 1} \right)\\t = \sqrt 2 \to {M_2}\left( {\sqrt 2 ; - \sqrt 2 - 1} \right)\end{array} \right.\)
Hướng dẫn giải:
- Gọi tọa độ điểm \(M\) theo tham số \(t\) thuộc đường thẳng \(d\).
- Từ điều kiện hai tiếp tuyến vuông góc suy ra tính chất \(MAIB\) là hình vuông.
- Từ đó lập phương trình ẩn \(t\), giải phương trình và kết luận.
Câu hỏi khác
- Bài tập một số khái niệm phương trình đường thẳng toán 10 có lời giải
- Bài tập vị trí tương đối của đường thẳng với đường tròn toán 10 có lời giải
- Bài tập một số bài toán viết phương trình đường thẳng toán 10 có lời giải
- Bài tập phương trình đường tròn toán 10 có lời giải
- Bài tập khoảng cách và góc toán 10 có lời giải
