Đặt: \(\left\{ \begin{array}{l}a = {x^2}\\b = 1 - {x^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a + b = 1\\a - b = 2{x^2} - 1\end{array} \right..\)
Khi đó: \(y = 32{x^2}\left( {1 - {x^2}} \right){\left( {2{x^2} - 1} \right)^2} = 32ab{\left( {a - b} \right)^2} = 32ab\left[ {{{\left( {a + b} \right)}^2} - 4ab} \right]\)
\( = 32ab\left( {1 - 4ab} \right) = 32ab - 128{a^2}{b^2} = - {\left( {8\sqrt 2 ab - \sqrt 2 } \right)^2} + 2 \le 2\) với mọi x
Dấu “=” xảy ra \( \Leftrightarrow 8\sqrt 2 ab = \sqrt 2 \Leftrightarrow ab = \dfrac{1}{8} \Leftrightarrow {x^2}\left( {1 - {x^2}} \right) = \dfrac{1}{8}\)
\( \Leftrightarrow {x^2} - {x^4} = \dfrac{1}{8} \Leftrightarrow \left[ \begin{array}{l}{x^2} = \dfrac{{2 + \sqrt 2 }}{4}\\{x^2} = \dfrac{{2 - \sqrt 2 }}{4}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \sqrt {\dfrac{{2 + \sqrt 2 }}{4}} \in \left( { - 1;1} \right)\\x = - \sqrt {\dfrac{{2 + \sqrt 2 }}{4}} \in \left( { - 1;1} \right)\\x = \sqrt {\dfrac{{2 - \sqrt 2 }}{4}} \in \left( { - 1;1} \right)\\x = - \sqrt {\dfrac{{2 - \sqrt 2 }}{4}} \in \left( { - 1;1} \right)\end{array} \right.\)
Vậy có 4 giá trị của \({x_0}\) thỏa mãn yêu cầu đề bài.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = {x^4} - 4{x^3} - {x^2} + 10x - 3$ trên đoạn $\left[ { - 1;4} \right]$ là
Ta có $y = {x^4} - 4{x^3} - {x^2} + 10x - 3$$ = {x^4} - 4{x^3} + 4{x^2} - 5{x^2} + 10x - 5 + 2$
$ = {\left( {{x^2} - 2x} \right)^2} - 5{\left( {x - 1} \right)^2} + 2$$ = {\left[ {{{\left( {x - 1} \right)}^2} - 1} \right]^2} - 5{\left( {x - 1} \right)^2} + 2$.
Đặt $t = {\left( {x - 1} \right)^2}$, $x \in \left[ { - 1;4} \right] \Rightarrow t \in \left[ {0;9} \right]$.
$y = {\left( {t - 1} \right)^2} - 5t + 2$$ = {t^2} - 7t + 3$$ = {\left( {t - \dfrac{7}{2}} \right)^2} - \dfrac{{37}}{4}$.
Ta có $0 \le {\left( {t - \dfrac{7}{2}} \right)^2} \le \dfrac{{121}}{4}$$ \Leftrightarrow - \dfrac{{37}}{4} \le y \le 21$.
Giá trị nhỏ nhất của biểu thức \(F = y - x\) trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\) là
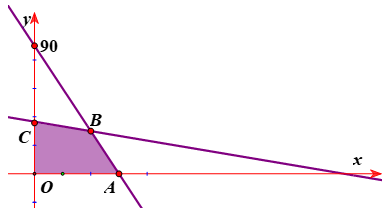
Miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\) là miền trong của tam giác $ABC$ kể cả biên (như hình)

Ta thấy \(F = y - x\) đạt giá trị nhỏ nhất chỉ có thể tại các điểm \(A\), \(B\), \(C\).
Tại \(A\left( {0; 2} \right)\) thì \(F = 2\).
Tại \(B\left( {1; 4} \right)\) thì \(F = 3\)
Tại \(A\left( {2; 3} \right)\) thì \(F = 1\).
Vậy \(\min F = 1\) khi \(x = 2\), \(y = 3\).
Cho bất phương trình: \({x^2} + 2\left| {x + m} \right| + 2mx + 3{m^2} - 3m + 1 < 0\). Để bất phương trình có nghiệm, các giá trị thích hợp của tham số \(m\) là
Phương trình đã cho tương đương: \({\left( {x + m} \right)^2} + 2\left| {x + m} \right| + 2{m^2} - 3m + 1 < 0\), \(\left( 1 \right)\).
Đặt \(t = \left| {x + m} \right|\), \(t \ge 0\).
Bất phương trình \(\left( 1 \right)\) trở thành: \({t^2} + 2t + 2{m^2} - 3m + 1 < 0\), \(\left( 2 \right)\).
Ta có: \(\Delta ' = - 2{m^2} + 3m\).
Nếu \(\Delta ' \le 0\) thì vế trái \(\left( 2 \right)\) luôn lớn hơn hoặc bằng \(0\), nên loại trường hợp này.
Nếu \(\Delta ' > 0\)\( \Leftrightarrow 0 < m < \dfrac{3}{2}\), \(\left( * \right)\), thì tam thức bậc \(2\) ở vế trái có \(2\) nghiệm phân biệt \({t_1} = - 1 - \sqrt { - 2{m^2} + 3m} \), \({t_2} = - 1 + \sqrt { - 2{m^2} + 3m} \).
Khi đó bất phương trình \(\left( 2 \right)\)\( \Leftrightarrow {t_1} < t < {t_2}\), mà điều kiện \(t \ge 0\).
Vậy để bất phương trình có nghiệm thì \({t_2} > 0\)\( \Leftrightarrow - 1 + \sqrt { - 2{m^2} + 3m} > 0\)\( \Leftrightarrow \sqrt { - 2{m^2} + 3m} > 1\)\( \Leftrightarrow - 2{m^2} + 3m - 1 > 0\)\( \Leftrightarrow \dfrac{1}{2} < m < 1\).
So với điều kiện \(\left( * \right)\), suy ra \(\dfrac{1}{2} < m < 1\).
Xác định \(m\) để phương trình \(\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0\) có ba nghiệm phân biệt lớn hơn \( - 1\).
\(\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} + 2\left( {m + 3} \right)x + 4m + 12 = 0{\rm{ }}\left( * \right)\end{array} \right.\).
Phương trình đã cho có ba nghiệm phân biệt lớn hơn \( - 1\) khi và chỉ khi khi phương trình \(\left( * \right)\) có hai nghiệm phân biệt ${x_1}$, ${x_2}$ lớn hơn \( - 1\) và khác \(1\)
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{x_1} + 1 + {x_2} + 1 > 0\\\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) > 0\\1 + 2\left( {m + 3} \right) + 4m + 12 \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 2m - 3 > 0\\ - 2m - 4 > 0\\2m + 7 > 0\\m \ne - \dfrac{{19}}{6}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} - \dfrac{7}{2} < m < - 3\\m \ne - \dfrac{{19}}{6}\end{array} \right.\).
Số nghiệm của phương trình $\sqrt {x + 8 - 2\sqrt {x + 7} } = 2 - \sqrt {x + 1 - \sqrt {x + 7} } $ là
$\sqrt {x + 8 - 2\sqrt {x + 7} } = 2 - \sqrt {x + 1 - \sqrt {x + 7} } $$ \Leftrightarrow \left\{ \begin{array}{l}\left| {\sqrt {x + 7} - 1} \right| = 2 - \sqrt {\left( {\sqrt {x + 7} - 3} \right)\left( {\sqrt {x + 7} + 2} \right)} \\\sqrt {x + 7} \ge 3\end{array} \right.$
$ \Leftrightarrow \left\{ \begin{array}{l}\sqrt {x + 7} - 3 + \sqrt {\left( {\sqrt {x + 7} - 3} \right)\left( {\sqrt {x + 7} + 2} \right)} = 0\\x \ge 2\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}\sqrt {\sqrt {x + 7} - 3} \left( {\sqrt {\sqrt {x + 7} - 3} + \sqrt {\sqrt {x + 7} + 2} } \right) = 0\\x \ge 2\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}\sqrt {x + 7} - 3 = 0\\x \ge 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\x \ge 2\end{array} \right. \Leftrightarrow x = 2$.
Tìm \(m\) để \(\left( {m + 1} \right){x^2} + mx + m < 0;\forall x \in \mathbb{R}\)?
Đặt \(f\left( x \right) = \left( {m + 1} \right){x^2} + mx + m\)
Xét \(m + 1 = 0 \Leftrightarrow m = - 1\) khi đó \(f\left( x \right) = - x - 1 < 0 \Leftrightarrow x > - 1\) \( \Rightarrow \) không thỏa mãn yêu cầu bài toán
Xét \(m + 1 \ne 0 \Leftrightarrow m \ne - 1\) khi đó \(f\left( x \right) < 0,\,\forall x \in \mathbb{R}\) \( \Leftrightarrow \) \(\left\{ \begin{array}{l}m + 1 < 0\\\Delta = {m^2} - 4m\left( {m + 1} \right) < 0\end{array} \right.\)
\( \Leftrightarrow \) \(\left\{ \begin{array}{l}m + 1 < 0\\m\left( {3m + 4} \right) > 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m < - 1\\\left[ \begin{array}{l}m < - \dfrac{4}{3}\\m > 0\end{array} \right.\end{array} \right.\) \( \Leftrightarrow m < - \dfrac{4}{3}\).
Tập nghiệm của bất phương trình \(2{x^2} + 4x + 3\sqrt {3 - 2x - {x^2}} > 1\) là
Đặt \(t = \sqrt {3 - 2x - {x^2}} \ge 0\) \( \Rightarrow {x^2} + 2x = 3 - {t^2}\).
Bất phương trình cho trở thành: \( - 2{t^2} + 3t + 5 > 0\)\( \Leftrightarrow - 1 < t < \dfrac{5}{2}\).
Suy ra \(0 \le \sqrt {3 - 2x - {x^2}} < \dfrac{5}{2}\)\( \Leftrightarrow \left\{ \begin{array}{l}0 \le 3 - 2x - {x^2}\\3 - 2x - {x^2} < \dfrac{{25}}{4}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} - 3 \le x \le 1\\x \in \mathbb{R}\end{array} \right.\) \( \Leftrightarrow - 3 \le x \le 1\).
Tìm giá trị lớn nhất của \(m\) để bất phương trình \(3\left( {x - m} \right) \ge {m^2}\left( {5 - x} \right)\) thỏa với mọi \(x \ge 5\).
\(3\left( {x - m} \right) \ge {m^2}\left( {5 - x} \right)\)\( \Leftrightarrow \left( {{m^3} + 3} \right)x \ge 5{m^2} + 3m\)\( \Leftrightarrow x \ge \dfrac{{5{m^2} + 3m}}{{{m^2} + 3}}\) vì \({m^2} + 3 > 0\).
Bất phương trình \(3\left( {x - m} \right) \ge {m^2}\left( {5 - x} \right)\)thỏa với mọi \(x \ge 5\) \( \Leftrightarrow \dfrac{{5{m^2} + 3m}}{{{m^3} + 3}} \le 5\)\( \Leftrightarrow m \le 5\)
Vậy giá trị lớn nhất của \(m\) là \(m = 5\).
Cho các số thực \(x\),\(y\) thỏa mãn: \(2\left( {{x^2} + {y^2}} \right) = 1 + xy\). Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = 7\left( {{x^4} + {y^4}} \right) + 4{x^2}{y^2}\) có tổng là
Ta có \(P = 7\left( {{x^4} + {y^4}} \right) + 4{x^2}{y^2}\)
\( = 7\left[ {\left( {{x^2} + {y^2}} \right) - 2{x^2}{y^2}} \right] + 4{x^2}{y^2}\)
\( = 7\left( {{x^2} + {y^2}} \right) - 10{x^2}{y^2}\)
\( = \dfrac{7}{4}{\left[ {2\left( {{x^2} + {y^2}} \right)} \right]^2} - 10{x^2}{y^2}\)
\( = \dfrac{7}{4}{\left( {1 + xy} \right)^2} - 10{x^2}{y^2} = \dfrac{7}{4} + \dfrac{7}{2}xy - \dfrac{{33}}{4}{\left( {xy} \right)^2}\)
Theo giả thiết, \(2\left( {{x^2} + {y^2}} \right) = 1 + xy \Rightarrow 2\left[ {{{\left( {x + y} \right)}^2} - 2xy} \right] = 1 + xy\)
\( \Rightarrow 5xy + 1 = 2{\left( {x + y} \right)^2} \ge 0 \Rightarrow xy \ge - \dfrac{1}{5}\,\,\left( * \right)\)
Lại có \(2\left( {{x^2} + {y^2}} \right) \ge 4xy \Rightarrow 1 + xy \ge 4xy \Rightarrow xy \le \dfrac{1}{3}\,\,\left( {**} \right)\)
Từ \(\left( * \right)\) và \(\left( {**} \right)\) suy ra \(xy \in \left[ { - \dfrac{1}{5};\dfrac{1}{3}} \right]\).
Đặt \(t = xy\), suy ra \(t \in \left[ { - \dfrac{1}{5};\dfrac{1}{3}} \right]\).
Khi đó \(P = - \dfrac{{33}}{4}{t^2} + \dfrac{7}{2}t + \dfrac{7}{4}\) với \(t \in \left[ { - \dfrac{1}{5};\dfrac{1}{3}} \right]\).
Ta có bảng biến thiên:

Dựa vào bảng biến thiên, suy ra GTLN của \(P\) là \(M = \dfrac{{70}}{{33}}\) và GTNN của \(P\) là \(m = \dfrac{{18}}{{25}}\).
Vậy \(M + m = \dfrac{{18}}{{25}} + \dfrac{{70}}{{33}} = \dfrac{{2344}}{{825}}\).
Một hình chữ nhật \(ABCD\) có \(AB = 8\) và \(AD = 6\). Trên đoạn \(AB\) lấy điểm \(E\) thỏa \(BE = 2\) và trên \(CD\) lấy điểm \(G\) thỏa \(CG = 6\). Người ta cần tìm một điểm \(F\) trên đoạn \(BC\) sao cho \(ABCD\) được chia làm hai phần màu trắng và màu xám như hình vẽ. Và diện tích phần màu xám bé hơn ba lần diện tích phần màu trắng. Điều kiện cần và đủ của điểm \(F\) là


Gọi \(BF = x > 0\), ta có \({S_{BEF}} + {S_{GFC}}\) \( = \dfrac{1}{2}BE.BF + \dfrac{1}{2}CF.CG\) \( = x + 3\left( {6 - x} \right) = 18 - 2x\).
\({S_{ABCD}} = AB.AD\)\( = 48\). Theo yêu cầu bài toán: \({S_{BEF}} + {S_{GFC}} > \dfrac{1}{4}{S_{ABCD}} \Leftrightarrow \)\(18 - 2x > \dfrac{1}{4}.48\)
\( \Leftrightarrow 2x < 6\)\( \Leftrightarrow x < 3\).
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm \(I\) và \(II\). Mỗi sản phẩm \(I\) bán lãi \(500\) nghìn đồng, mỗi sản phẩm \(II\) bán lãi \(400\) nghìn đồng. Để sản xuất được một sản phẩm \(I\) thì Chiến phải làm việc trong \(3\) giờ, Bình phải làm việc trong \(1\) giờ. Để sản xuất được một sản phẩm \(II\) thì Chiến phải làm việc trong \(2\) giờ, Bình phải làm việc trong \(6\) giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá \(180\) giờ và Bình không thể làm việc quá \(220\) giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là.
Gọi \(x\), \(y\) lần lượt là số sản phẩm loại \(I\) và loại \(II\) được sản xuất ra. Điều kiện \(x\), \(y\) nguyên dương.
Ta có hệ bất phương trình sau: \(\left\{ \begin{array}{l}3x + 2y \le 180\\x + 6y \le 220\\x > 0\\y > 0\end{array} \right.\)
Miền nghiệm của hệ trên là
Tiền lãi trong một tháng của xưởng là \(T = 0,5x + 0,4y\) (triệu đồng).
Ta thấy \(T\) đạt giá trị lớn nhất chỉ có thể tại các điểm \(A\), \(B\), \(C\). Vì \(C\) có tọa độ không nguyên nên loại.
Tại \(A\left( {60; 0} \right)\) thì \(T = 30\) triệu đồng.
Tại \(B\left( {40; 30} \right)\) thì \(T = 32\) triệu đồng.
Vậy tiền lãi lớn nhất trong một tháng của xưởng là \(32\) triệu đồng.
Cho các số thực dương \(x\), \(y\), \(z\). Giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2} + {y^2} + {z^2}}}{{xy + 2yz + zx}}\) là
Ta có \(2yz \le {y^2} + {z^2}\)
Dấu “=” xảy ra khi \(y = z\).
Suy ra \(P \ge \dfrac{{{x^2} + {y^2} + {z^2}}}{{xy + xz + {y^2} + {z^2}}} = Q\)
Khi \(y = z\), ta có \(Q = \dfrac{{{x^2} + 2{y^2}}}{{2xy + 2{y^2}}} = \dfrac{{{{\left( {\dfrac{x}{y}} \right)}^2} + 2}}{{{{\left( {\dfrac{x}{y}} \right)}^2} + 2}}\).
\( \Leftrightarrow {\left( {\dfrac{x}{y}} \right)^2} - 2P\left( {\dfrac{x}{y}} \right) + 2 - 2P = 0\) \(\left( * \right)\) (do \(P > 0\))
Để tồn tại \(\dfrac{x}{y}\) thì \(\Delta ' = {P^2} + 2P - 2 \ge 0 \Rightarrow P \ge \sqrt 3 - 1\).
Vậy \({P_{\min }} = \sqrt 3 - 1\) khi \(\dfrac{x}{y} = \sqrt 3 - 1\) và \(y = z\).
Cho các số dương \(x\), \(y\), \(z\) thỏa mãn \(xyz = 1\). Khi đó giá trị nhỏ nhất của biểu thức\(P = \dfrac{{\sqrt {1 + {x^3} + {y^3}} }}{{xy}} + \dfrac{{\sqrt {1 + {y^3} + {z^3}} }}{{yz}} + \dfrac{{\sqrt {1 + {z^3} + {x^3}} }}{{zx}}\) là
Áp dụng BĐT Cô-si, ta có: \(1 + {x^3} + {y^3} \ge 3xy\)\( \Rightarrow \dfrac{{\sqrt {1 + {x^3} + {y^3}} }}{{xy}} \ge \dfrac{{\sqrt 3 }}{{\sqrt {xy} }}\) \( = \sqrt {3z} \).
Tương tự, ta có: \(\dfrac{{\sqrt {1 + {y^3} + {z^3}} }}{{yz}} \ge \sqrt {3x} \), \(\dfrac{{\sqrt {1 + {z^3} + {x^3}} }}{{zx}} \ge \sqrt {3y} \).
Suy ra: \(P \ge \sqrt {3x} + \sqrt {3y} + \sqrt {3z} \) \( \ge 3\sqrt 3 \sqrt[3]{{\sqrt {xyz} }}\) \( = 3\sqrt 3 \).
Dấu đẳng thức xảy ra \( \Leftrightarrow x = y = z = 1\).
Vậy \(\min P = 3\sqrt 3 \).

