Phương trình \(\sqrt {{x^3} - 4{x^2} + 5x - 2} + x = \sqrt {2 - x} \) có bao nhiêu nghiệm ?
\(\begin{array}{l}\left\{ \begin{array}{l}{x^3} - 4{x^2} + 5x - 2 \ge 0\\2 - x \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^3} - 4{x^2} + 4x + x - 2 \ge 0\\x \le 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x\left( {{x^2} - 4x + 4} \right) + \left( {x - 2} \right) \ge 0\\x \le 2\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x{\left( {x - 2} \right)^2} + \left( {x - 2} \right) \ge 0\\x \le 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 2} \right)\left( {{x^2} - 2x + 1} \right) \ge 0\\x \le 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 2} \right){\left( {x - 1} \right)^2} \ge 0\\x \le 2\end{array} \right.\end{array}\)
Do \(\left\{ \begin{array}{l}{\left( {x - 1} \right)^2} \ge 0\\x \le 2 \Leftrightarrow x - 2 \le 0\end{array} \right. \\\Rightarrow \left( {x - 2} \right){\left( {x - 1} \right)^2} \le 0\)
Mà \(\left( {x - 2} \right){\left( {x - 1} \right)^2} \ge 0 \Leftrightarrow \) dấu "=" xảy ra \( \Leftrightarrow \left( {x - 2} \right){\left( {x - 1} \right)^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\).
Thử lại với \(x = 1\) ta có \(\sqrt 0 + 1 = \sqrt 1 \) (đúng)
Với \(x = 2\) ta có \(\sqrt 0 + 2 = \sqrt 0 \) (vô lí)
Vậy phương trình đã cho có 1 nghiệm \(x = 1\).
Tìm tất cả các giá trị của tham số m để phương trình \(2\left( {{x^2} - 2x} \right) + \sqrt {\left( {x + 1} \right)\left( {3 - x} \right)} - m = 0\) có hai nghiệm phân biệt.
Điều kiện: \( - 1 \le x \le 3.\)
Ta có: \(2\left( {{x^2} - 2x} \right) + \sqrt {\left( {x + 1} \right)\left( {3 - x} \right)} - m = 0\)\( \Leftrightarrow 2\left( {{x^2} - 2x} \right) + \sqrt { - {x^2} + 2x + 3} - m = 0\,\,\,\,\left( * \right)\)
Đặt \(t = \sqrt { - {x^2} + 2x + 3} \,\,\,\,\left( {t \ge 0} \right)\) thay vào phương trình \(\left( * \right)\) ta được:
\(2\left( {3 - {t^2}} \right) + t - m = 0\)\( \Leftrightarrow - 2{t^2} + t + 6 = m\) \(\left( {**} \right)\)
Xét \({t^2} = - {x^2} + 2x + 3\,\,\,\left( {***} \right)\) ta có BBT:
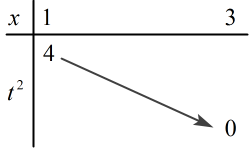
\( \Rightarrow \) Với \(x \in \left[ {1;\,\,3} \right]\) ta có: \({t^2} \in \left[ {0;\,\,4} \right]\) \( \Rightarrow t \in \left[ { - 2;\,\,2} \right]\)
Lại có: \(t \ge 0\) \( \Rightarrow t \in \left[ {0;\,\,2} \right]\)
Để phương \(\left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \left( {***} \right)\) có hai nghiệm phân biệt \( \Leftrightarrow t \in \left[ {0;\,\,2} \right).\)
Đặt \(f\left( t \right) = - 2{t^2} + t + 6\).
Ta có BBT của hàm số \(y = f\left( t \right)\)
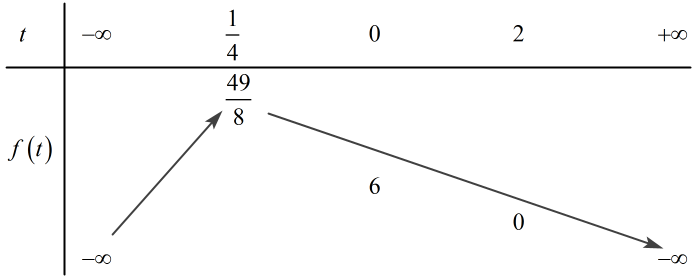
\( \Rightarrow \) Để phương trình \(\left( {**} \right)\) có nghiệm \(t\) thỏa mãn \(0 \le t < 2\) thì đường thẳng \(y = m\) phải cắt đồ thị hàm số \(f\left( t \right)\)
Dựa vào BBT ta thấy đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( t \right)\) trên \(\left[ {0;\,\,2} \right)\) \( \Leftrightarrow 0 < m \le 6.\)
Vậy với \(m \in \left( {0;6} \right]\) thì phương trình đã cho có hai nghiệm phân biệt.
Cho phương trình \({x^3} + 3{x^2} + \left( {4{m^2} - 12m + 11} \right)x + {\left( {2m - 3} \right)^2} = 0.\) Tập hợp tất cả các giá trị của tham số m để phương trình có 3 nghiệm phân biệt.
\(\begin{array}{l}{x^3} + 3{x^2} + \left( {4{m^2} - 12m + 11} \right)x + {\left( {2m - 3} \right)^2} = 0\left( * \right)\\ \Leftrightarrow \,{x^3} + 3{x^2} + \left( {4{m^2} - 12m + 11} \right)x + 4{m^2} - 12m + 9 = 0\\ \Leftrightarrow {x^3} + {x^2} + 2{x^2} + 2x + \left( {4{m^2} - 12m + 9} \right)x + 4{m^2} - 12m + 9 = 0\\ \Leftrightarrow {x^2}\left( {x + 1} \right) + 2x\left( {x + 1} \right) + \left( {4{m^2} - 12m + 9} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 2x + 4{m^2} - 12m + 9} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\g\left( x \right) = {x^2} + 2x + 4{m^2} - 12m + 9 = 0\end{array} \right.\end{array}\)
Phương trình đã cho có 3 nghiệm phân biệt \( \Leftrightarrow g\left( x \right) = 0\) có hai nghiệm phân biệt \( \ne - 1\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\g\left( { - 1} \right) \ne 0\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}1 - 4{m^2} + 12m - 9 > 0\\{\left( { - 1} \right)^2} + 2\left( { - 1} \right) + 4{m^2} - 12m + 9 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 12m + 8 < 0\\4{m^2} - 12m + 8 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 < m < 2\\m \ne 2\\m \ne 1\end{array} \right.\\ \Leftrightarrow 1 < m < 2.\end{array}\)
Có tất cả bao nhiêu giá trị nguyên không dương của tham số $m$ để phương trình $\sqrt {2x + m} = x - 1$ có nghiệm duy nhất?
$\sqrt {2x + m} = x - 1$$ \Leftrightarrow \left\{ \begin{array}{l}x - 1 \ge 0\\2x + m = {\left( {x - 1} \right)^2}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 4x + 1 - m = 0\left( * \right)\end{array} \right.$.
Phương trình có nghiệm duy nhất khi hệ có nghiệm duy nhất.
Xét ${x^2} - 4x + 1 - m = 0$; \(\Delta ' = 3 + m\)
TH1: \(\Delta ' = 0 \Leftrightarrow m = - 3\) thì (*) có nghiệm kép \(x = 2 \ge 1\) (thỏa).
TH2: \(\Delta ' > 0 \Leftrightarrow m > - 3\) thì phương trình có nghiệm duy nhất khi (*) có 2 nghiệm thỏa \({x_1} < 1 < {x_2}\) \( \Leftrightarrow \left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) < 0 \Leftrightarrow {x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1 < 0\) \( \Leftrightarrow 1 - m - 4 + 1 < 0 \Leftrightarrow m > - 2\).
Do $m$ không dương nên $m\in \{-1;0\}$
Kết hợp với trường hợp $m=-3$ ở trên ta được $3$ giá trị của $m$ thỏa mãn bài toán.
Giả sử phương trình $2{x^2} - 4mx - 1 = 0$ (với \(m\) là tham số) có hai nghiệm \({x_1}\), \({x_2}\). Tìm giá trị nhỏ nhất của biểu thức $T = \left| {{x_1} - {x_2}} \right|$.
Phương trình $2{x^2} - 4mx - 1 = 0$ có $\Delta ' = 4{m^2} + 2 > 0$ nên phương trình có hai nghiệm phân biệt \({x_1}\), \({x_2}\) với $S = {x_1} + {x_2} = 2m$, $P = {x_1}{x_2} = - \dfrac{1}{2}$.
Ta có ${T^2} = {\left( {{x_1} - {x_2}} \right)^2}$ $ = {S^2} - 4P$$ = 4{m^2} + 2 \ge 2$$ \Rightarrow T \ge \sqrt 2 $.
Dấu bằng xảy ra khi $m = 0$.
Vậy \(\min T = \sqrt 2 \).
Gọi \(S\) là tập hợp các giá trị của tham số \(m\) sao cho parabol \(\left( P \right)\): \(y = {x^2} - 4x + m\) cắt \(Ox\) tại hai điểm phân biệt \(A\), \(B\) thỏa mãn \(OA = 3OB\). Tính tổng \(T\) các phần tử của $S$.
Phương trình hoành độ giao điểm của $\left( P \right)$ và $Ox$: \({x^2} - 4x + m = 0\) (1)
Để $\left( P \right)$ cắt $Ox$ tại hai điểm phân biệt thì (1) có hai nghiệm phân biệt ${x_1}$, ${x_2}$
$ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\a \ne 0\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}4 - m > 0\\1 \ne 0\end{array} \right.$$ \Leftrightarrow m < 4$.
Giả sử $A\left( {{x_1};0} \right)$, $B\left( {{x_2};0} \right)$ và ${x_1} + {x_2} = 4$, ${x_1}{x_2} = m$.
Ta có \(OA = 3OB\)\( \Leftrightarrow \left| {{x_1}} \right| = 3\left| {{x_2}} \right|\)$ \Leftrightarrow \left[ \begin{array}{l}{x_1} = 3{x_2}\\{x_1} = - 3{x_2}\end{array} \right.$.
Trường hợp 1: \({x_1} = 3{x_2}\)$ \Rightarrow \left\{ \begin{array}{l}{x_1} = 3\\{x_2} = 1\end{array} \right.$$ \Rightarrow m = 3$ (thỏa mãn)
Trường hợp 2: \({x_1} = - 3{x_2}\)$ \Rightarrow \left\{ \begin{array}{l}{x_1} = 6\\{x_2} = - 2\end{array} \right.$$ \Rightarrow m = - 12$ (thỏa mãn)
Vậy $S = - 12 + 3 = - 9$.
Phương trình \(\sqrt[3]{{x + 5}} + \sqrt[3]{{x + 6}} = \sqrt[3]{{2x + 11}}\) có bao nhiêu nghiệm.
\(\sqrt[3]{{x + 5}} + \sqrt[3]{{x + 6}} = \sqrt[3]{{2x + 11}}\)
\( \Leftrightarrow x + 5 + x + 6 + 3\sqrt[3]{{x + 5}}\sqrt[3]{{x + 6}}\left( {\sqrt[3]{{x + 5}} + \sqrt[3]{{x + 6}}} \right) = 2x + 11\)
\( \Rightarrow 3\sqrt[3]{{x + 5}}\sqrt[3]{{x + 6}}\sqrt[3]{{2x + 11}} = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = - 5\\x = - 6\\x = - \dfrac{{11}}{2}\end{array} \right.\)
Thử lại $3$ giá trị $-5;-6;- \dfrac{{11}}{2}$ đều thỏa mãn phương trình.
Vậy phương trình đã cho có $3$ nghiệm phân biệt.
Tập nghiệm của phương trình \(\sqrt[4]{{x - \sqrt {{x^2} - 1} }} + \sqrt {x + \sqrt {{x^2} - 1} } = 2\) là
Đặt \(t = \sqrt[4]{{x - \sqrt {{x^2} - 1} }},t > 0\)
\(\sqrt[4]{{x - \sqrt {{x^2} - 1} }} = t\) \( \Rightarrow {t^2} = \sqrt {x - \sqrt {{x^2} - 1} } \) \( = \sqrt {\dfrac{{\left( {x - \sqrt {{x^2} - 1} } \right)\left( {x + \sqrt {{x^2} - 1} } \right)}}{{x + \sqrt {{x^2} - 1} }}} \) \( = \sqrt {\dfrac{{{x^2} - {x^2} + 1}}{{x + \sqrt {{x^2} - 1} }}} \) \( = \sqrt {\dfrac{1}{{x + \sqrt {{x^2} - 1} }}} \) \( = \dfrac{1}{{\sqrt {x + \sqrt {{x^2} - 1} } }}\) \( \Rightarrow \sqrt {x + \sqrt {{x^2} - 1} } = \dfrac{1}{{{t^2}}}\)
Ta có pt: \(t + \dfrac{1}{{{t^2}}} = 2\) \( \Leftrightarrow {t^3} - 2{t^2} + 1 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = \dfrac{{1 + \sqrt 5 }}{2}\\t = \dfrac{{1 - \sqrt 5 }}{2}\end{array} \right.\)
So sánh với điều kiện $t > 0$ ta tìm được \(t = 1,\)\(t = \dfrac{{1 + \sqrt 5 }}{2}\)
Trường hợp 1: \(t = 1:\sqrt[4]{{x - \sqrt {{x^2} - 1} }} = 1\)\( \Leftrightarrow x - \sqrt {{x^2} - 1} = 1\)
\( \Leftrightarrow x - 1 = \sqrt {{x^2} - 1} \)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 2x + 1 = {x^2} - 1\end{array} \right. \Leftrightarrow x = 1\)
Trường hợp 2: \(t = \dfrac{{1 + \sqrt 5 }}{2}\)\( \Rightarrow \sqrt[4]{{x - \sqrt {{x^2} - 1} }} = \dfrac{{1 + \sqrt 5 }}{2}\)
\( \Leftrightarrow x - \sqrt {{x^2} - 1} = \dfrac{{7 + 3\sqrt 5 }}{2}\)\( \Leftrightarrow x - \dfrac{{7 + 3\sqrt 5 }}{2} = \sqrt {{x^2} - 1} \)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{{7 + 3\sqrt 5 }}{2}\\{\left( {x - \dfrac{{7 + 3\sqrt 5 }}{2}} \right)^2} = {x^2} - 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{{7 + 3\sqrt 5 }}{2}\\x = \dfrac{7}{2}\end{array} \right.\) \( \Rightarrow x \in \emptyset \)
Kết hợp hai trường hợp ta được nghiệm $x=1$.
Tìm $m$ để phương trình \(\left( {m - 1} \right){x^4} - m{x^2} + {m^2} - 1 = 0\) có ba nghiệm phân biệt.
+ Khi $m - 1 = 0$$ \Leftrightarrow m = 1$ phương trình cho trở thành: \( - {x^2} = 0\)\( \Leftrightarrow x = 0\)
Do đó: $m = 1$ không thỏa mãn đề bài.
+ Khi $m - 1 \ne 0$$ \Leftrightarrow m \ne 1$
Đặt \(t = {x^2}\)\(\left( {t \ge 0} \right)\).
Phương trình cho trở thành \(\left( {m - 1} \right){t^2} - mt + {m^2} - 1 = 0\,\,\,\,\left( 1 \right)\).
Phương trình cho có ba nghiệm phân biệt \( \Leftrightarrow \left( 1 \right)\) có hai nghiệm \({t_1},\,{t_2}\) thoả ${t_1} = 0 < {t_2}$
Khi \({t_1} = 0 \Rightarrow m = \pm 1\). Do có hai nghiệm phân biệt nên \(m \ne 1\).
Với \(m = - 1 \Rightarrow {t_2} = \dfrac{1}{2}\) (nhận).
Phương trình \({x^4} - 5{x^3} + 8{x^2} - 10x + 4 = 0\) có bao nhiêu nghiệm nguyên?
\({x^4} - 5{x^3} + 8{x^2} - 10x + 4 = 0\)\( \Leftrightarrow \left( {{x^4} + 4{x^2} + 4} \right) - 5{x^3} + 4{x^2} - 10x = 0\) \( \Leftrightarrow {\left( {{x^2} + 2} \right)^2} - \left( {5{x^3} + 10x} \right) + 4{x^2} = 0\) \( \Leftrightarrow {\left( {{x^2} + 2} \right)^2} - 5x\left( {{x^2} + 2} \right) + 4{x^2} = 0\)
Đặt \(t = {x^2} + 2\) ta được \({t^2} - 5tx + 4{x^2} = 0 \Leftrightarrow \left( {t - x} \right)\left( {t - 4x} \right) = 0\)
Hay phương trình đã cho \( \Leftrightarrow \left( {{x^2} - x + 2} \right)\left( {{x^2} - 4x + 2} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} - x + 2 = 0\left( {VN} \right)\\{x^2} - 4x + 2 = 0\end{array} \right. \Leftrightarrow x = 2 \pm \sqrt 2 \)
Vậy phương trình không có nghiệm nguyên.
Cho hàm số \(y = {x^2} - 2x - 2\) có đồ thị \(\left( P \right)\), và đường thẳng \(\left( d \right)\) có phương trình \(y = x + m\). Tìm $m$ để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\), \(B\) sao cho \(O{A^2} + O{B^2}\) đạt giá trị nhỏ nhất.
Phương trình hoành độ giao điểm: \({x^2} - 2x - 2 = x + m\)\( \Leftrightarrow {x^2} - 3x - 2 - m = 0\)
\(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\), \(B\)\( \Leftrightarrow \Delta > 0 \Leftrightarrow 17 + 4m > 0\) \( \Leftrightarrow m > - \dfrac{{17}}{4}\).
Giả sử \(\left( * \right)\) có hai nghiệm \({x_1},{x_2}\) thì \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a} = 3\\{x_1}{x_2} = \dfrac{c}{a} = - m - 2\end{array} \right.\)
$A\left( {{x_1};{x_1} + m} \right)$ $ \Rightarrow \overrightarrow {OA} = \left( {{x_1};{x_1} + m} \right)$
$B\left( {{x_2};{x_2} + m} \right)$$ \Rightarrow \overrightarrow {OB} = \left( {{x_2};{x_2} + m} \right)$
\(O{A^2} + O{B^2} = x_1^2 + x_2^2 + {\left( {{x_1} + m} \right)^2} + {\left( {{x_2} + m} \right)^2}\)\( = 2{\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} + 2m\left( {{x_1} + {x_2}} \right) + 2{m^2}\)
\( = 18 - 4\left( { - 2 - m} \right) + 6m + 2{m^2}\)\( = 2{m^2} + 10m + 26\)\( = 2{\left( {m + \dfrac{5}{2}} \right)^2} + \dfrac{{27}}{2} \ge \dfrac{{27}}{2}\) với \(m > - \dfrac{{17}}{4}\)
Vậy giá trị nhỏ nhất của \(O{A^2} + O{B^2}\) là \(\dfrac{{27}}{2}\) khi \(m = - \dfrac{5}{2}\).
Số nghiệm của phương trình \({x^2} - 2x - 8 = 4\sqrt {\left( {4 - x} \right)\left( {x + 2} \right)} \) là
Điều kiện: \(\left( {4 - x} \right)\left( {x + 2} \right) \ge 0 \Leftrightarrow x \in \left[ { - 2;\,4} \right]\)
\({x^2} - 2x - 8 = 4\sqrt {\left( {4 - x} \right)\left( {x + 2} \right)} \)\( \Leftrightarrow {x^2} - 2x - 8 = 4\sqrt { - \left( {{x^2} - 2x - 8} \right)} \left( 1 \right)\)
Đặt \(t = \sqrt { - \left( {{x^2} - 2x - 8} \right)} \), \(t \ge 0\) \( \Leftrightarrow {t^2} = - \left( {{x^2} - 2x - 8} \right)\)\( \Leftrightarrow {x^2} - 2x - 8 = - {t^2}\)
\(\left( 1 \right) \Leftrightarrow - {t^2} = 4t\)\( \Leftrightarrow {t^2} + 4t = 0\)\( \Leftrightarrow \left[ \begin{array}{l}t = 0\left( n \right)\\t = - 4\left( l \right)\end{array} \right.\) \( \Leftrightarrow \sqrt { - \left( {{x^2} - 2x - 8} \right)} = 0\)\( \Leftrightarrow - \left( {{x^2} - 2x - 8} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 2\left( TM \right)\\x = 4\left( TM \right)\end{array} \right.\)
Vậy phương trình đã cho có hai nghiệm.
Tập hợp tất cả các giá trị của tham số \(m\) để phương trình \(\sqrt {1 + x} + \sqrt {1 - x} + 4\sqrt {1 - {x^2}} = m\) có nghiệm là
\(\sqrt {1 + x} + \sqrt {1 - x} + 4\sqrt {1 - {x^2}} = m\)\(\left( 1 \right)\)
Điều kiện: \( - 1 \le x \le 1\).
Đặt \(t = \sqrt {1 + x} + \sqrt {1 - x} \ge 0 \)\( \Rightarrow {t^2} = 2 + 2\sqrt {1 - {x^2}} \)
Do $2\le t^2\le 4$ nên \( t \in \left[ {\sqrt 2 ;\,2} \right]\).
\(\left( 1 \right)\) trở thành \(t + 2\left( {{t^2} - 2} \right) = m\)\( \Leftrightarrow 2{t^2} + t - \left( {4 + m} \right) = 0\) \(\left( 2 \right)\).
Để \(\left( 1 \right)\) có nghiệm thì \(\left( 2 \right)\) có nghiệm \(t \in \left[ {\sqrt 2 ;\,2} \right]\)
Tức là $\left\{ \begin{array}{l}\Delta = 1 + 4.2\left( {4 + m} \right) = 8m + 33 \ge 0\\\left[ \begin{array}{l}\sqrt 2 \le \dfrac{{ - 1 - \sqrt {8m + 33} }}{4} \le 2\\\sqrt 2 \le \dfrac{{ - 1 + \sqrt {8m + 33} }}{4} \le 2\end{array} \right.\end{array} \right.$\( \Leftrightarrow \left\{ \begin{array}{l}m \ge - \dfrac{{33}}{8}\\4\sqrt 2 + 1 \le \sqrt {8m + 33} \le 9\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \ge - \dfrac{{33}}{8}\\\sqrt 2 \le m \le 6\end{array} \right.\)\( \Leftrightarrow \sqrt 2 \le m \le 6\).
Vậy \(m \in \left[ {\sqrt 2 ;\,6} \right]\) thì phương trình đã cho có nghiệm.
Cho phương trình ${x^3} - \left( {2m + 1} \right){x^2} + \left( {4m - 1} \right)x - 2m + 1 = 0.$ Tìm $m$ để phương trình có một nghiệm duy nhất?
Ta có ${x^3} - \left( {2m + 1} \right){x^2} + \left( {4m - 1} \right)x - 2m + 1 = 0$ $\left( 1 \right)$$ \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2mx + 2m - 1} \right) = 0$
$ \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2mx + 2m - 1 = 0\left( * \right)\end{array} \right.$.
Để pt $\left( 1 \right)$ có một nghiệm duy nhất thì pt $\left( * \right)$ có nghiệm kép $x = 1$
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {m^2} - 2m + 1 = 0\\1 - 2m + 2m - 1 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 1} \right)^2} = 0\\0 = 0\end{array} \right. \Leftrightarrow m = 1\)
Tổng bình phương các nghiệm của phương trình \({x^2} + 5x + 2 + 2\sqrt {{x^2} + 5x + 10} = 0\) là
Điều kiện xác định \({x^2} + 5x + 10 \ge 0 \Leftrightarrow x \in \mathbb{R}\).
Khi đó phương trình \( \Leftrightarrow {x^2} + 5x + 10 + 2\sqrt {{x^2} + 5x + 10} - 8 = 0\) $ \Leftrightarrow \left( {\sqrt {{x^2} + 5x + 10} - 2} \right)\left( {\sqrt {{x^2} + 5x + 10} + 4} \right) = 0$
\( \Leftrightarrow \left[ \begin{array}{l}\sqrt {{x^2} + 5x + 10} = 2\\\sqrt {{x^2} + 5x + 10} = - 4(VN)\end{array} \right.\) \( \Leftrightarrow \sqrt {{x^2} + 5x + 10} = 2 \Leftrightarrow {x^2} + 5x + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}{x} = - 3\\{x} = - 2\end{array} \right.\)
Vậy \(x_1^2 + x_2^2 = {2^2} + {3^2} = 13\).
Tìm tất cả các giá trị của \(m\) để phương trình \({x^2} - 2x - 3 - m = 0\) có nghiệm \(x \in \left[ {0;4} \right]\).
Phương trình đã cho tương đương \(m = {x^2} - 2x - 3\).
Đặt \(y = f\left( x \right) = {x^2} - 2x - 3\).
Ta có đồ thị hàm số \(y = f\left( x \right)\) như sau:
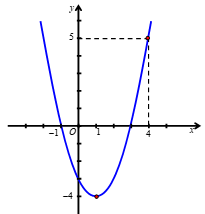
Dựa vào đồ thị, để phương trình \(y = f\left( x \right) = {x^2} - 2x - 3 = m\) có nghiệm \(x \in \left[ {0;4} \right]\) thì \( - 4 \le m \le 5\)
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) có đồ thị như hình vẽ.
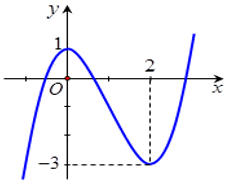
Phương trình \(2f\left( x \right) - 1 = 0\) có bao nhiêu nghiệm?
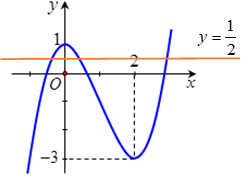
Phương trình đã cho tương đương \(f\left( x \right) = \dfrac{1}{2}\)
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = \dfrac{1}{2}\)
Quan sát đồ thị hàm số ta thấy đường thẳng \(y = \dfrac{1}{2}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại đúng \(3\) điểm phân biệt.
Vậy phương trình \(2f\left( x \right) - 1 = 0\) có \(3\) nghiệm phân biệt.
Tổng các bình phương các nghiệm của phương trình $\left( {x - 1} \right)\left( {x - 3} \right) + 3\sqrt {{x^2} - 4x + 5} - 2 = 0$ là
Ta có $\left( {x - 1} \right)\left( {x - 3} \right) + 3\sqrt {{x^2} - 4x + 5} - 2 = 0$
$ \Leftrightarrow {x^2} - 4x + 5 + 3\sqrt {{x^2} - 4x + 5} - 4 = 0$\( \Leftrightarrow \left( {\sqrt {{x^2} - 4x + 5} - 1} \right)\left( {\sqrt {{x^2} - 4x + 5} + 4} \right) = 0\) $ \Leftrightarrow \left[ \begin{array}{l}\sqrt {{x^2} - 4x + 5} = 1\\\sqrt {{x^2} - 4x + 5} = - 4(VN)\end{array} \right.$
$ \Leftrightarrow $${x^2} - 4x + 5 = 1$ $\Leftrightarrow {x^2} - 4x + 4 = 0 \Leftrightarrow x = 2$.
Vậy tổng bình phương các nghiệm là $2^2=4$
Tìm phương trình đường thẳng \(d:y = ax + b\). Biết đường thẳng \(d\) đi qua điểm \(I\left( {1\,;\,3} \right)\) và tạo với hai tia \(Ox\), \(Oy\) một tam giác có diện tích bằng \(6\)?
Do đường thẳng \(d\) đi qua điểm \(I\left( {1\,;\,3} \right)\) nên \(a + b = 3\)\( \Rightarrow a = 3 - b\).
Giao điểm của \(d\) và các tia \(Ox\), \(Oy\) lần lượt là \(M\left( { - \dfrac{b}{a}\,;\,0} \right)\) và \(N\left( {0\,;\,b} \right)\)
(với \(b > 0\), \(a < 0\) suy ra \( b > 3\)).
Do đó: \({S_{\Delta OMN}} = \dfrac{1}{2}.OM.ON\)\( = \dfrac{1}{2}.\left| {\dfrac{b}{a}} \right|.\left| b \right| = \dfrac{{{b^2}}}{{2\left| a \right|}}\). Mà \({S_{\Delta OMN}} = 6\)\( \Leftrightarrow {b^2} = 12\left| a \right|\)\( \Leftrightarrow {b^2} = 12\left| {3 - b} \right|\)\( \Leftrightarrow \left[ \begin{array}{l}{b^2} = 36 - 12b\\{b^2} = - 36 + 12b\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}b = 6(TM)\\b = - 6 + \sqrt {72} \;\left( {\rm{L}} \right)\\b = - 6 - \sqrt {72} \,\,{\rm{(L)}}\end{array} \right.\).
Với \(b = 6\)\( \Rightarrow a = - 3\)\( \Rightarrow d:y = - 3x + 6\)

