Tìm tất cả các giá trị của tham số m để phương trình 2(x2−2x)+√(x+1)(3−x)−m=0 có hai nghiệm phân biệt.
Trả lời bởi giáo viên
Điều kiện: −1≤x≤3.
Ta có: 2(x2−2x)+√(x+1)(3−x)−m=0⇔2(x2−2x)+√−x2+2x+3−m=0(∗)
Đặt t=√−x2+2x+3(t≥0) thay vào phương trình (∗) ta được:
2(3−t2)+t−m=0⇔−2t2+t+6=m (∗∗)
Xét t2=−x2+2x+3(∗∗∗) ta có BBT:
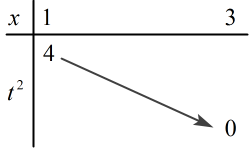
⇒ Với x∈[1;3] ta có: t2∈[0;4] ⇒t∈[−2;2]
Lại có: t≥0 ⇒t∈[0;2]
Để phương (∗) có hai nghiệm phân biệt ⇔(∗∗∗) có hai nghiệm phân biệt ⇔t∈[0;2).
Đặt f(t)=−2t2+t+6.
Ta có BBT của hàm số y=f(t)
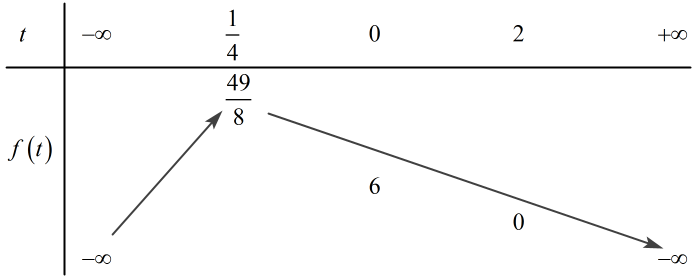
⇒ Để phương trình (∗∗) có nghiệm t thỏa mãn 0≤t<2 thì đường thẳng y=m phải cắt đồ thị hàm số f(t)
Dựa vào BBT ta thấy đường thẳng y=m cắt đồ thị hàm số y=f(t) trên [0;2) ⇔0<m≤6.
Vậy với m∈(0;6] thì phương trình đã cho có hai nghiệm phân biệt.
Hướng dẫn giải:
Sử dụng phương pháp đặt ẩn phụ, điều kiện để có 2 nghiệm phân biệt và phương pháp hình học.

