Câu hỏi:
3 năm trước
Tìm tất cả các giá trị của \(m\) để phương trình \({x^2} - 2x - 3 - m = 0\) có nghiệm \(x \in \left[ {0;4} \right]\).
Trả lời bởi giáo viên
Đáp án đúng: c
Phương trình đã cho tương đương \(m = {x^2} - 2x - 3\).
Đặt \(y = f\left( x \right) = {x^2} - 2x - 3\).
Ta có đồ thị hàm số \(y = f\left( x \right)\) như sau:
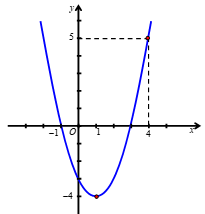
Dựa vào đồ thị, để phương trình \(y = f\left( x \right) = {x^2} - 2x - 3 = m\) có nghiệm \(x \in \left[ {0;4} \right]\) thì \( - 4 \le m \le 5\)
Hướng dẫn giải:
Sử dụng phương pháp hàm số, xét hàm \(y = {x^2} - 2x - 3\) trên \(\left[ {0;4} \right]\) rồi nhận xét điều kiện có nghiệm của phương trình.

