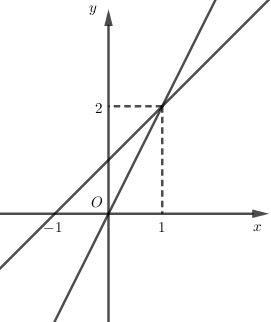
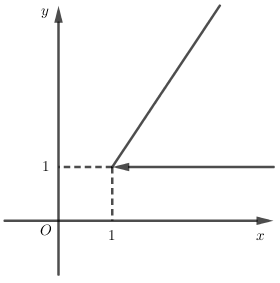
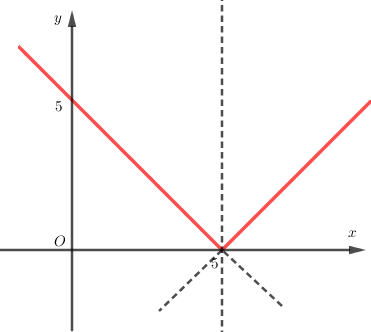
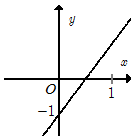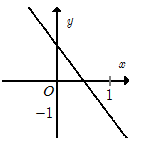Hàm số \(y = x + \left| x \right|\) được viết lại là
Nếu \(x \ge 0\) thì \(\left| x \right| = x\) nên \(x + \left| x \right| = x + x = 2x\).
Nếu \(x < 0\) thì \(\left| x \right| = - x\) nên \(x + \left| x \right| = x + \left( { - x} \right) = 0\).
\(y = x + \left| x \right| = \left\{ \begin{array}{l}2x\,\,\,khi\,\,\,x \ge 0\\0\,\,\,\,\,\,khi\,\,\,\,x < 0\end{array} \right.\).
Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi hàm số đó là hàm số nào?
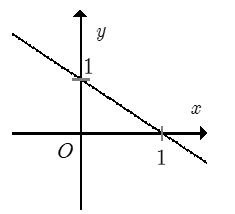
Đồ thị đi xuống từ trái sang phải \( \Rightarrow \) hệ số góc \(a < 0.\) Loại A, C.
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0;1} \right).\)
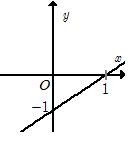
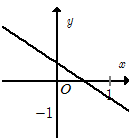
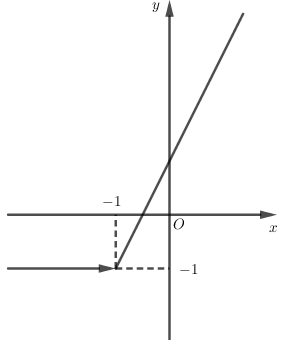
Hàm số \(y = 2x - 1\) có đồ thị là hình nào trong bốn hình sau?
Giao điểm của đồ thị hàm số \(y = 2x - 1\) với trục hoành là \(\left( {\dfrac{1}{2};0} \right).\) Loại B.
Giao điểm của đồ thị hàm số \(y = 2x - 1\) với trục tung là \(\left( {0; - 1} \right).\)Chỉ có A thỏa mãn.
Cho hàm số \(y = f\left( x \right) = - \dfrac{{2x}}{3} + \dfrac{1}{2}\) có đồ thị là $(d)$. Mệnh đề nào sau đây là đúng?
Xét \(y = f\left( x \right) = - \dfrac{{2x}}{3} + \dfrac{1}{2}\)
Cho \(y = 0 \Rightarrow 0 = - \dfrac{2}{3}x + \dfrac{1}{2} \Leftrightarrow x = 3 \)
\(\Rightarrow \) Đồ thị hàm số cắt trục hoành tại điểm \(\left( {3;0} \right)\)
Ta có: \(1 = - \dfrac{2}{3}.\dfrac{1}{2} + 1\) (vô lý) \( \Rightarrow A\left( {\dfrac{1}{2};1} \right) \notin d\)
Ta có: \(a = - \dfrac{2}{3} < 0 \Rightarrow \) Hàm số \(y = f\left( x \right) \) nghịch biến trên R.
Điểm nào dưới đây thuộc đồ thị hàm số \(y = 3x - 1\).
Ta có \(5 = 2.3 - 1 \Rightarrow \) Điểm \(\left( {2;5} \right)\) thuộc đồ thị hàm số \(y = 3x - 1\).
Tìm a để đường thẳng \(y = ax - 1\) đi qua điểm \(M\left( {1;3} \right)\).
Thay điểm M vào phương trình đường thẳng ta có: \(3 = a - 1 \Leftrightarrow a = 4\).
Xác định vị trí tương đối của 2 đường thẳng sau: \({\Delta _1}:\,x - 27y + 2018 = 0,\) \({\Delta _2}: - 3x + 6y - 20 = 0\).
\({\Delta _1}:\,x - 27y + 2018 = 0 \)\(\Leftrightarrow y=\dfrac{1}{27}x+\dfrac{2018}{27}\)
\(\,{\Delta _2}: - 3x + 6y - 20 = 0\)\(\Leftrightarrow y=\dfrac{1}{2}x+\dfrac{10}{3}\)
Ta có: \(\dfrac{1}{{27}} \ne \dfrac{{1}}{2} \Rightarrow {\Delta _1}\) cắt \(\,{\Delta _2}\).
Mặt khác: \(\dfrac{1}{{27}}.\dfrac{{1}}{2}\ne -1 \Rightarrow {\Delta _1}\) không vuông góc\(\,{\Delta _2}\).
Vậy \({\Delta _1}\) và\(\,{\Delta _2}\) cắt nhau nhưng không vuông góc.
Cho hai đường thẳng \({d_1}:y = x + 100\) và \({d_2}:y = \dfrac{1}{2}x + 100.\) Mệnh đề nào sau đây đúng?
Ta có: \({d_1}:\,\,y = x + 100;\,\,\,{d_2}:\,\,y = \dfrac{1}{2}x + 100\) có: \({a_1} = 1 \ne {a_2} = \dfrac{1}{2}\) và \({a_1}.{a_2} = 1.\dfrac{1}{2} \ne 1 \Rightarrow {d_1},\,\,{d_2}\) cắt nhau nhưng không vuông góc với nhau.
Hàm số $y = \left| {x + 2} \right| - 4x$ bằng hàm số nào sau đây?
Ta có: $y = \left| {x + 2} \right| - 4x$.
+) Nếu \(x + 2 \ge 0 \Leftrightarrow x \ge - 2\) thì \(y = x + 2 - 4x = - 3x + 2\).
+) Nếu \(x + 2 < 0 \Leftrightarrow x < - 2\) thì \(y = - x - 2 - 4x = - 5x - 2\).
Vậy $y = \left\{ \begin{array}{l} - 3x + 2\,\,\,\,khi\,\,\,x \ge - 2\\ - 5x - 2\,\,\,\,khi\,\,\,x < - 2\end{array} \right.$.
Hàm số $y = \left| {x + 1} \right| + \left| {x - 3} \right|$ được viết lại là
Ta có bảng:
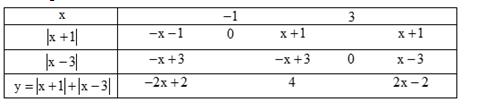
Từ bảng trên ta có kết luận: $y = \left\{ \begin{array}{l} - 2x + 2\,\,\,\,khi\,\,\,x \le - 1\\4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\, - 1 < x \le 3\\2x - 2\,\,\,\,\,\,khi\,\,\,\,x > 3\end{array} \right.$
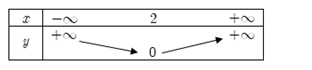
Cho hàm số $y = \left| {2x - 4} \right|$. Bảng biến thiên nào sau đây là bảng biến thiên của hàm số đã cho
- Ta có: $y = \left| {2x - 4} \right| = \left\{ \begin{array}{l}2x - 4\,\,\,\,khi\,\,\,x \ge 2\\ - 2x + 4\,khi\,x < 2\end{array} \right.$
- Hàm số \(y = 2x - 4\) luôn đồng biến và \(y = - 2x + 4\) luôn nghịch biến nên ta có:
Bảng biến thiên:
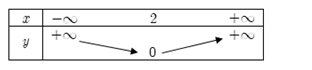
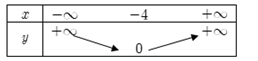
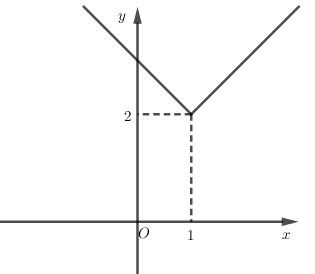
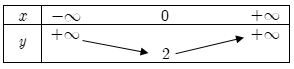
Hàm số $y = \left| x \right| + 2$ có bảng biến thiên nào sau đây?
- Ta có: $y = \left| x \right| + 2 = \left\{ \begin{array}{l}x + 2\,\,\,\,khi\,\,\,x \ge 0\\ - x + 2\,khi\,\,\,x < 0\end{array} \right.$
- Hàm số \(y = x + 2\) luôn đồng biến và hàm số \(y = - x + 2\) luôn nghịch biến nên ta có:
Bảng biến thiên:
Đồ thị sau đây biểu diễn hàm số nào?
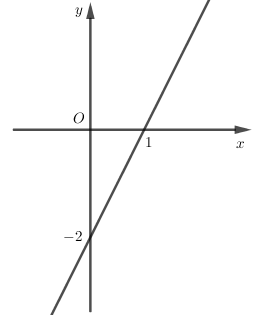
Gọi hàm số \(y = ax + b\left( {a \ne 0} \right)\).
Điểm \(A\left( {1;0} \right),B\left( {0; - 2} \right)\) thuộc đồ thị hàm số
\( \Leftrightarrow \) tọa độ của chúng thỏa mãn hệ phương trình:
\(\left\{ \begin{array}{l}0 = a.1 + b\\ - 2 = a.0 + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 2\\a = 2\end{array} \right. \Rightarrow y = 2x - 2\).
Đồ thị sau đây biểu diễn hàm số nào?
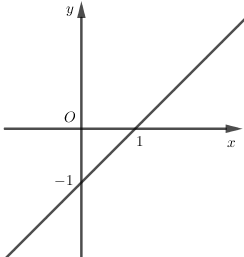
Điểm \(A\left( {1;0} \right),B\left( {0; - 1} \right)\) thuộc đồ thị hàm số
\( \Leftrightarrow \) tọa độ của chúng thỏa mãn hệ phương trình:
\(\left\{ \begin{array}{l}0 = a.1 + b\\ - 1 = a.0 + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 1\\a = 1\end{array} \right. \Rightarrow y = x - 1\).
Đồ thị sau đây biểu diễn hàm số nào?
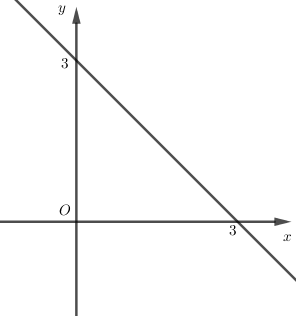
Điểm \(A\left( {3;0} \right),B\left( {0;3} \right)\) thuộc đồ thị hàm số
\( \Leftrightarrow \) tọa độ của chúng thỏa mãn hệ phương trình:
\(\left\{ \begin{array}{l}0 = a.3 + b\\3 = a.0 + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\a = - 1\end{array} \right. \Rightarrow y = - x + 3\).
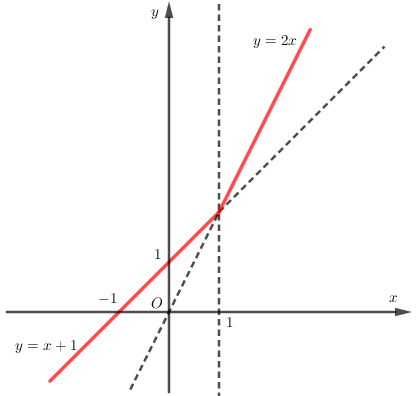
Hàm số $y = \left\{ \begin{array}{l}2x \text{ khi } x \ge 1\\x + 1 \text{ khi } x < 1\end{array} \right.$ có đồ thị
Ta có đồ thị hàm số $y = \left\{ \begin{array}{l}2x\text{ khi }x \ge 1\\x + 1\text{ khi }x < 1\end{array} \right.$ như sau:
Đồ thị sau đây biểu diễn hàm số nào?
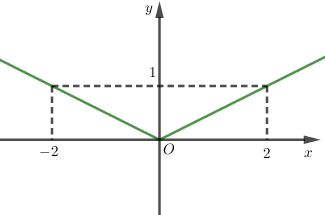
- Đồ thị hàm số đi qua hai điểm \(A\left( { - 2;1} \right)\) và \(B\left( {2;1} \right)\).
- Thay tọa độ \(A\) vào đáp án A ta được: \(1 = \left| { - 2} \right|\) (loại).
- Thay tọa độ \(A\) vào đáp án B ta được: \(1 = \left| {2.\left( { - 2} \right)} \right|\) (loại).
- Thay tọa độ \(A\) và \(B\) vào đáp án C ta được: \(1 = \left| {\dfrac{1}{2}.\left( { - 2} \right)} \right|\) và \(1 = \left| {\dfrac{1}{2}.2} \right|\) nên C thỏa mãn.
- Thay tọa độ $A$ vào đáp án D ta được: \(1 = \left| {3 - \left( { - 2} \right)} \right|\) (loại).
Đồ thị sau đây biểu diễn hàm số nào?
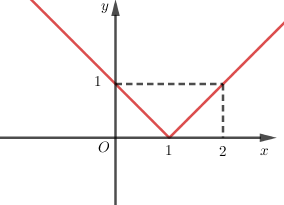
- Đồ thị hàm số đi qua các điểm \(A\left( {0;1} \right),B\left( {1;0} \right),C\left( {2;1} \right)\).
- Ta thấy:
+) Tọa độ \(B\) không thỏa đáp án A vì \(0 \ne \left| {1 + 1} \right|\), loại A.
+) Tọa độ cả ba điểm \(A,B,C\) đều thỏa B nên B thỏa mãn.
+) Tọa độ \(B\) không thỏa mãn C vì \(0 \ne \left| 1 \right| + 1\), loại C.
+) Tọa độ \(A\) không thỏa mãn D vì \(1 \ne \left| 0 \right| - 1\), loại D.
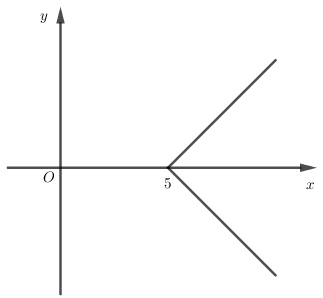
Hàm số $y = \left| {x - 5} \right|$ có đồ thị nào trong các đồ thị sau đây?
- Ta có: $y = \left| {x - 5} \right| = \left\{ \begin{array}{l}x - 5\,\,\,\,\,khi\,\,\,x \ge 5\\ - x + 5\,\,khi\,\,x < 5\end{array} \right.$.
- Vẽ đồ thị hàm số $y = \left\{ \begin{array}{l}x - 5\,\,\,\,\,khi\,\,\,x \ge 5\\ - x + 5\,\,khi\,\,x < 5\end{array} \right.$.
+ Vẽ hai đường thẳng \(y = x - 5\) và \(y = - x + 5\) trên cũng một hệ trục tọa độ.
+ Giữ nguyên phần đồ thị bên phải đường thẳng \(x = 5\) của đồ thị hàm số \(y = x - 5\) và xóa phần bên trái.
+ Giữ nguyên phần đồ thị bên trái đường thẳng \(x = 5\) của đồ thị hàm số \(y = - x + 5\) và xóa phần bên phải.
Từ đó ta có đồ thị hàm số $y = \left\{ \begin{array}{l}x - 5\,\,\,\,\,khi\,\,\,x \ge 5\\ - x + 5\,\,khi\,\,x < 5\end{array} \right.$ là:
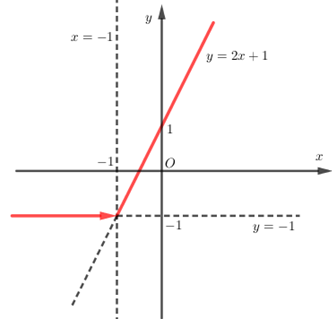
Hàm số $y = x + \left| {x + 1} \right|$có đồ thị là
- Ta có: $y = x + \left| {x + 1} \right| = \left\{ \begin{array}{l}2x + 1\,\,\,\,khi\,\,\,\,x \ge - 1\\ - 1\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\,x < - 1\end{array} \right.$
- Vẽ đồ thị hàm số $y = \left\{ \begin{array}{l}2x + 1\,\,\,\,khi\,\,\,\,x \ge - 1\\ - 1\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\,x < - 1\end{array} \right.$
+ Vẽ đồ thị hàm số \(y = 2x + 1\) và \(y = - 1\) trên cùng một hệ trục tọa độ.
+ Giữ nguyên phần đồ thị \(y = 2x + 1\) bên phải đường thẳng \(x = - 1\) và xóa phần bên trái.
+ Giữ nguyên phần đồ thị \(y = - 1\) bên trái đường thẳng \(x = - 1\) và xóa phần bên phải.
Khi đó ta có đồ thị sau: