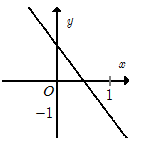Trả lời bởi giáo viên
Đáp án đúng: b
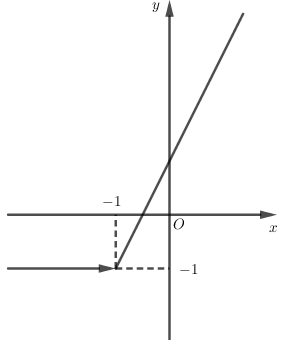
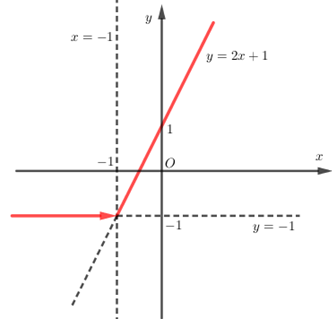
- Ta có: y=x+|x+1|={2x+1khix≥−1−1khix<−1
- Vẽ đồ thị hàm số y={2x+1khix≥−1−1khix<−1
+ Vẽ đồ thị hàm số y=2x+1 và y=−1 trên cùng một hệ trục tọa độ.
+ Giữ nguyên phần đồ thị y=2x+1 bên phải đường thẳng x=−1 và xóa phần bên trái.
+ Giữ nguyên phần đồ thị y=−1 bên trái đường thẳng x=−1 và xóa phần bên phải.
Khi đó ta có đồ thị sau:
Hướng dẫn giải:
- Viết lại hàm số y=x+|x+1| dưới dạng khoảng.
- Vẽ đồ thị hàm số thu được và kết luận.