Câu hỏi:
2 năm trước
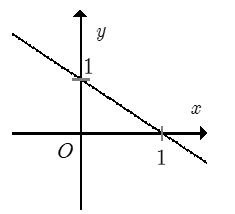
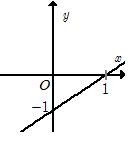
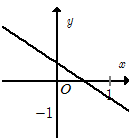
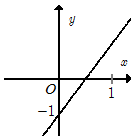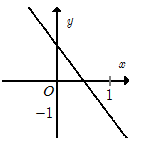Cho hàm số \(y = f\left( x \right) = - \dfrac{{2x}}{3} + \dfrac{1}{2}\) có đồ thị là $(d)$. Mệnh đề nào sau đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng: d
Xét \(y = f\left( x \right) = - \dfrac{{2x}}{3} + \dfrac{1}{2}\)
Cho \(y = 0 \Rightarrow 0 = - \dfrac{2}{3}x + \dfrac{1}{2} \Leftrightarrow x = 3 \)
\(\Rightarrow \) Đồ thị hàm số cắt trục hoành tại điểm \(\left( {3;0} \right)\)
Ta có: \(1 = - \dfrac{2}{3}.\dfrac{1}{2} + 1\) (vô lý) \( \Rightarrow A\left( {\dfrac{1}{2};1} \right) \notin d\)
Ta có: \(a = - \dfrac{2}{3} < 0 \Rightarrow \) Hàm số \(y = f\left( x \right) \) nghịch biến trên R.
Hướng dẫn giải:
Hàm số bậc nhất \(y = ax + b\,\,\left( {a \ne 0} \right)\)
+) Đồng biến trên R nếu \(a > 0\), nghịch biến trên R nếu \(a < 0\).
+) Cắt trục hoành tại điểm \(\left( { - \dfrac{b}{a};0} \right)\), cắt trục tung tại điểm \(\left( {0;b} \right)\).
