Xét ba đường thẳng sau: $2x-y + 1 = 0$;$x + 2y-17 = 0$;$x + 2y-3 = 0$. Chọn kết luận đúng:
- Ta có:
$\begin{array}{l}2x-y + 1 = 0 \Leftrightarrow y = 2x + 1\\x + 2y-17 = 0 \Leftrightarrow y = - \dfrac{1}{2}x + \dfrac{{17}}{2}\\x + 2y-3 = 0 \Leftrightarrow y = - \dfrac{1}{2}x + \dfrac{3}{2}\end{array}$
Dễ thấy hai đường thẳng sau có \( - \dfrac{1}{2} = - \dfrac{1}{2}\) và \(\dfrac{{17}}{2} \ne \dfrac{3}{2}\) nên chúng song song.
Lại có \( - \dfrac{1}{2}.2 = - 1\) nên đường thẳng thứ nhất vuông góc với cả hai đường thẳng sau.
Cho hàm số \(y = ax + b\) có đồ thị là hình bên. Giá trị của $a$ và $b$ là:
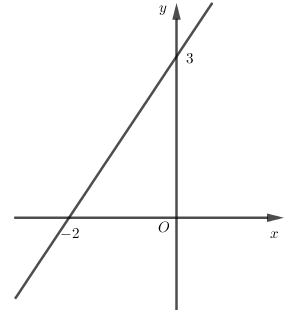
Điểm \(A\left( { - 2;0} \right),B\left( {0;3} \right)\) thuộc đồ thị hàm số thì tọa độ của chúng thỏa mãn hệ phương trình:
\(\left\{ \begin{array}{l}0 = a.\left( { - 2} \right) + b\\3 = a.0 + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\a = \dfrac{3}{2}\end{array} \right.\).
Hàm số $y = 2x - \dfrac{3}{2}$ có đồ thị là hình nào trong bốn hình sau
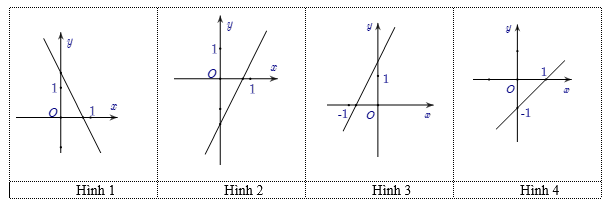
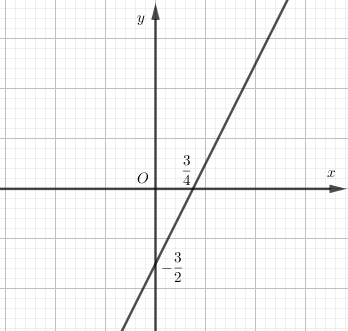
Vẽ đồ thị hàm số $y = 2x - \dfrac{3}{2}$ trên hệ trục tọa độ:
- Cho \(x = 0 \Rightarrow y = - \dfrac{3}{2} \Rightarrow A\left( {0; - \dfrac{3}{2}} \right)\).
- Cho \(y = 0 \Rightarrow x = \dfrac{3}{4} \Rightarrow B\left( {\dfrac{3}{4};0} \right)\).
Nối hai điểm \(A,B\) ta được đồ thị hàm số cần tìm.
Điểm nào sau đây thuộc đồ thị hàm số \(y = 2x - 3\)?
Ta có: \(2.\left( { - 2} \right) - 3 = - 4 - 3 = - 7 \Rightarrow P\left( { - 2; - 7} \right)\) thuộc đồ thị hàm số.

