ĐK: \(\left\{ \begin{array}{l}x - 2 \ge 0\\x + 2 \ge 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \ge - 2\end{array} \right.\) \( \Leftrightarrow x \ge 2\) \( \Rightarrow D = \left[ {2; + \infty } \right)\).
\(\begin{array}{l}\,\,\,\,\,4\sqrt {x - 2} + {m^2}\sqrt {x + 2} = 5\sqrt[4]{{{x^2} - 4}}\\ \Leftrightarrow 4\sqrt {x - 2} + {m^2}\sqrt {x + 2} = 5\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\end{array}\)
TH1: \(x = 2\), phương trình trở thành: \(2{m^2} = 0 \Leftrightarrow m = 0\).
Thử lại với \(m = 0\) ta có:
\(\begin{array}{l}4\sqrt {x - 2} = 5\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\\ \Leftrightarrow \sqrt[4]{{x - 2}}\left( {4\sqrt[4]{{x - 2}} - 5\sqrt[4]{{x + 2}}} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {tm} \right)\\4\sqrt[4]{{x - 2}} - 5\sqrt[4]{{x + 2}} = 0\end{array} \right.\end{array}\)
Do đó phương trình có nghiệm \(x = 2\), suy ra \(m = 0\) thỏa mãn.
TH2: \(x \ne 2\), chia cả 2 vế của phương trình cho \(\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\) ta được: \(4\dfrac{{\sqrt[4]{{x - 2}}}}{{\sqrt[4]{{x + 2}}}} + {m^2}\dfrac{{\sqrt[4]{{x + 2}}}}{{\sqrt[4]{{x - 2}}}} = 5\)
Đặt \(\dfrac{{\sqrt[4]{{x - 2}}}}{{\sqrt[4]{{x + 2}}}} = t\,\,\left( {0 < t < 1} \right)\), phương trình trở thành \(4t + \dfrac{{{m^2}}}{t} = 5\)\( \Leftrightarrow 4{t^2} - 5t + {m^2} = 0\) (*)
Phương trình (*) có nghiệm \( \Leftrightarrow \Delta = 25 - 16{m^2} \ge 0 \Leftrightarrow - \dfrac{5}{4} \le m \le \dfrac{5}{4}\).
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;0;1} \right\}\).
Thử lại:
Với \(m = \pm 1\) ta có: \(4{t^2} - 4t + 1 = 0 \Leftrightarrow t = \dfrac{1}{2}\).
\(\begin{array}{l} \Rightarrow \dfrac{{\sqrt[4]{{x - 2}}}}{{\sqrt[4]{{x + 2}}}} = \dfrac{1}{2}\\ \Leftrightarrow 2\sqrt[4]{{x - 2}} = \sqrt[4]{{x + 2}}\\ \Leftrightarrow 16\left( {x - 2} \right) = x + 2\\ \Leftrightarrow 16x - 32 = x + 2\\ \Leftrightarrow 15x = 34\\ \Leftrightarrow x = \dfrac{{34}}{{15}}\,\,\left( {tm} \right)\end{array}\)
\( \Rightarrow m = \pm 1\) thỏa mãn.
Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán là \(m \in \left\{ { - 1;0;1} \right\}\).
Tìm \(m\) để phương trình sau có nghiệm: \(\sqrt {3 + x} + \sqrt {6 - x} - \sqrt {\left( {3 + x} \right)\left( {6 - x} \right)} = m\).
ĐKXĐ: \( - 3 \le x \le 6\).
Đặt \(t = \sqrt {3 + x} + \sqrt {6 - x} \)
\(\begin{array}{l} \Rightarrow {t^2} = 3 + x + 6 - x + 2\sqrt {\left( {3 + x} \right)\left( {6 - x} \right)} \\ \Rightarrow {t^2} = 9 + 2\sqrt {\left( {3 + x} \right)\left( {6 - x} \right)} \\ \Rightarrow \sqrt {\left( {3 + x} \right)\left( {6 - x} \right)} = \dfrac{{{t^2} - 9}}{2}\end{array}\)
Do \(\sqrt {\left( {3 + x} \right)\left( {6 - x} \right)} \ge 0 \Leftrightarrow \dfrac{{{t^2} - 9}}{2} \ge 0\\ \Leftrightarrow \left[ \begin{array}{l}t \ge 3\\t \le - 3\end{array} \right. \Leftrightarrow t \ge 3\) (do \(t \ge 0\)).
Lại có \(\left( {3 + x} \right)\left( {6 - x} \right) = - {x^2} + 3x + 18 \le \dfrac{{81}}{4}\,\,\forall x\) nên \(\dfrac{{{t^2} - 9}}{2} \le \dfrac{9}{2} \Leftrightarrow t \le 3\sqrt 2 \).
\( \Rightarrow 3 \le t \le 3\sqrt 2 \).
Khi đó phương trình trở thành
\(t - \dfrac{{{t^2} - 9}}{2} = m \Leftrightarrow {t^2} - 2t + 2m - 9 = 0\,\,\left( * \right)\)
Để phương trình ban đầu có nghiệm thì phương trình (*) phải có nghiệm thỏa mãn (1).
Ta có \(\Delta ' = 1 - 2m + 9 = 10 - 2m \ge 0 \Leftrightarrow m \le 5\).
Khi đó phương trình (*) có nghiệm \(\left[ \begin{array}{l}{t_1} = 1 + \sqrt {10 - 2m} \\{t_2} = 1 - \sqrt {10 - 2m} \end{array} \right.\).
\(\begin{array}{l} \Rightarrow \left[ \begin{array}{l}3 \le 1 + \sqrt {10 - 2m} \le 3\sqrt 2 \\3 \le 1 - \sqrt {10 - 2m} \le 3\sqrt 2 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2 \le \sqrt {10 - 2m} \le 3\sqrt 2 - 1\\1 - 3\sqrt 2 \le \sqrt {10 - 2m} \le - 2\,\,\,\left( {VN} \right)\end{array} \right.\\ \Leftrightarrow 4 \le 10 - 2m \le 19 - 6\sqrt 2 \\ \Leftrightarrow 6\sqrt 2 - 9 \le 2m \le 6\\ \Leftrightarrow 3\sqrt 2 - \dfrac{9}{2} \le m \le 3\end{array}\)
Kết hợp điều kiện ta có \(3\sqrt 2 - \dfrac{9}{2} \le m \le 3\).
Tìm \(m\) để phương trình \(2x - 4 = 3\sqrt {x - m} \) có nghiệm.
ĐKXĐ: \(x - m \ge 0 \Leftrightarrow x \ge m\).
Ta có:
\(\begin{array}{l}2x - 4 = 3\sqrt {x - m} \\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\4{\left( {x - 2} \right)^2} = 9\left( {x - m} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\4{x^2} - 16x + 16 = 9x - 9m\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\4{x^2} - 25x + 9m + 16 = 0\,\,\left( * \right)\end{array} \right.\end{array}\)
Để phương trình ban đầu có nghiệm thì phương trình (*) phải có nghiệm \(x \ge 2\).
\(\begin{array}{l} \Rightarrow \Delta = {25^2} - 4.4\left( {9m + 16} \right) \ge 0\\ \Leftrightarrow 369 - 144m \ge 0 \Leftrightarrow m \le \dfrac{{41}}{{16}}\end{array}\)
Khi đó phương trình có 2 nghiệm \(x = \dfrac{{25 \pm \sqrt {369 - 144m} }}{8}\).
\(\begin{array}{l} \Rightarrow \left[ \begin{array}{l}\dfrac{{25 + \sqrt {369 - 144m} }}{8} \ge 2\\\dfrac{{25 - \sqrt {369 - 144m} }}{8} \ge 2\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt {369 - 144m} \ge - 9\,\,\,\left( {luon\,\,dung} \right)\\\sqrt {369 - 144m} \le 9\end{array} \right.\\ \Leftrightarrow 0 \le 369 - 144m \le 81\\ \Leftrightarrow 2 \le m \le \dfrac{{41}}{{16}}\end{array}\)
Kết hợp điều kiện \(\left\{ \begin{array}{l}x \ge 2\\x \ge m\end{array} \right.\) ta thấy \(2 \le m \le \dfrac{{41}}{{16}}\) thỏa mãn.
Vậy \(2 \le m \le \dfrac{{41}}{{16}}\).
Tìm \(m\) để phương trình sau có nghiệm
\(\sqrt x + \sqrt {9 - x} = \sqrt { - {x^2} + 9x + m} \)
ĐKXĐ: \(\left\{ \begin{array}{l}x \ge 0\\9 - x \ge 0\\ - {x^2} + 9x + m \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le x \le 9\\ - {x^2} + 9x + m \ge 0\end{array} \right.\).
Xét \( - {x^2} + 9x + m \ge 0 \Leftrightarrow - {x^2} + 9x \ge - m\).
Ta có \( - {x^2} + 9x = - \left( {{x^2} - 2.x.\dfrac{9}{2} + \dfrac{{81}}{4}} \right) + \dfrac{{81}}{4} = - {\left( {x - \dfrac{9}{2}} \right)^2} + \dfrac{{81}}{4} \le \dfrac{{81}}{4}\)
\( \Rightarrow - {x^2} + 9x \ge - m\) có nghiệm khi và chỉ khi \( - m \le \dfrac{{81}}{4} \Leftrightarrow m \ge - \dfrac{{81}}{4}\,\,\left( 1 \right)\).
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\sqrt x + \sqrt {9 - x} = \sqrt { - {x^2} + 9x + m} \\ \Rightarrow {\left( {\sqrt x + \sqrt {9 - x} } \right)^2} = - {x^2} + 9x + m\\ \Leftrightarrow x + 9 - x + 2\sqrt { - {x^2} + 9x} = - {x^2} + 9x + m\\ \Leftrightarrow 2\sqrt { - {x^2} + 9x} + 9 = - {x^2} + 9x + m\\ \Leftrightarrow \left( { - {x^2} + 9x} \right) - 2\sqrt { - {x^2} + 9x} + m - 9 = 0\,\,\,\left( * \right)\end{array}\)
Đặt \(t = \sqrt { - {x^2} + 9x} \) \( \Rightarrow 0 \le t \le \sqrt {\dfrac{{81}}{4}} \Rightarrow 0 \le t \le \dfrac{9}{2}\).
Khi đó phương trình (*) trở thành \({t^2} - 2t + m - 9 = 0\) có nghiệm \(t \in \left[ {0;\dfrac{9}{2}} \right]\).
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\Delta ' \ge 0\\0 \le {t_1} + {t_2} \le 9\\{t_1}{t_2} \ge 0\\\left( {{t_1} - \dfrac{9}{2}} \right)\left( {{t_2} - \dfrac{9}{2}} \right) \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}1 - m + 9 \ge 0\\0 \le 2 \le 9\,\,\left( {luon\,\,dung} \right)\\m - 9 \ge 0\\m - 9 - \dfrac{9}{2}.2 + \dfrac{{81}}{4} \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \le 10\\m \ge 9\\m \ge - \dfrac{9}{4}\end{array} \right. \Leftrightarrow 9 \le m \le 10\end{array}\)
Kết hợp điều kiện (1) ta có \(m \in \left[ {9;10} \right]\).
Tìm \(m\) để phương trình \(\sqrt {{x^2} + mx + 2} = 2x + 1\) có 2 nghiệm phân biệt.
Ta có:
\(\begin{array}{l}\sqrt {{x^2} + mx + 2} = 2x + 1\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - \dfrac{1}{2}\\{x^2} + mx + 2 = 4{x^2} + 4x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - \dfrac{1}{2}\\3{x^2} - \left( {m - 4} \right)x - 1 = 0\,\,\,\left( * \right)\end{array} \right.\end{array}\)
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt \({x_1} > {x_2} \ge - \dfrac{1}{2}\).
\(\begin{array}{l}\Rightarrow \left\{ \begin{array}{l}\Delta > 0\\{x_1} + {x_2} > - 1\\\left( {{x_1} + \dfrac{1}{2}} \right)\left( {{x_2} + \dfrac{1}{2}} \right) \ge 0\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 4} \right)^2} + 12 > 0\,\,\left( {luon\,\,dung} \right)\\\dfrac{{m - 4}}{3} > - 1\\ - \dfrac{1}{3} + \dfrac{1}{2}.\dfrac{{m - 4}}{3} + \dfrac{1}{4} \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m - 4 > - 3\\\dfrac{{m - 4}}{6} \ge \dfrac{1}{{12}}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 1\\m - 4 \ge \dfrac{1}{2}\end{array} \right. \Leftrightarrow m \ge \dfrac{9}{2}\end{array}\)
Vậy \(m \ge \dfrac{9}{2}\).
Hỏi có bao nhiêu giá trị $m$ nguyên trong đoạn $\left[ {0;2017} \right]$ để phương trình $\left| {{x^2} - 4\left| x \right| - 5} \right| - m = 0$ có hai nghiệm phân biệt?
PT: $\left| {{x^2} - 4} \right|x\left| { - 5} \right| - m = 0 \Leftrightarrow \left| {{x^2} - 4} \right|x\left| { - 5} \right| = m\left( 1 \right)$
Số nghiệm phương trình \(\left( 1 \right) \) bằng số giao điểm của đồ thị hàm số \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\,\left( P \right)\) và đường thẳng \(y = m\) (cùng phương \(Ox\))
Xét hàm số \(y = {x^2} - 4x - 5\,\,\left( {{P_1}} \right)\) có đồ thị như hình 1.
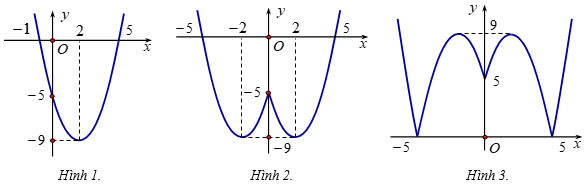
Xét hàm số \(y = {x^2} - 4\left| x \right| - 5\,\,\left( {{P_2}} \right)\) là hàm số chẵn nên có đồ thị nhận \(Oy\) làm trục đối xứng.
Mà \(y = {x^2} - 4\left| x \right| - 5 = {x^2} - 4x - 5\) nếu \(x \ge 0\).
Suy ra đồ thị hàm số \(\left( {{P_2}} \right)\) gồm hai phần:
Phần \(1\): Giữ nguyên đồ thị hàm số \(\left( {{P_1}} \right)\) phần bên phải \(Oy\).
Phần \(2\): Lấy đối xứng phần \(1\) qua trục \(Oy\).
Ta được đồ thị \(\left( {{P_2}} \right)\) như hình 2.
Xét hàm số \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\,\left( P \right)\), ta có: \(y = \left\{ \begin{array}{l}{x^2} - 4\left| x \right| - 5\,\,\,\,\,\,\,\,\,\,\left( {y \ge 0} \right)\\ - \left( {{x^2} - 4\left| x \right| - 5} \right)\,\,\left( {y < 0} \right)\end{array} \right.\).
Suy ra đồ thị hàm số \(\left( P \right)\) gồm hai phần:
Phần \(1\): Giữ nguyên đồ thị hàm số \(\left( {{P_2}} \right)\) phần trên \(Ox\).
Phần \(2\): Lấy đối xứng đồ thị hàm số \(\left( {{P_2}} \right)\) phần dưới \(Ox\) qua trục \(Ox\).
Ta được đồ thị \(\left( P \right)\) như hình 3.
Quan sát đồ thị hàm số \(\left( P \right)\) ta có:
Phương trình $\left| {{x^2} - 4\left| x \right| - 5} \right| - m = 0$ (1) có hai nghiệm phân biệt \( \Leftrightarrow \left[ \begin{array}{l}m > 9\\m = 0\end{array} \right.\).
Mà \(\left\{ \begin{array}{l}m \in \mathbb{Z}\\m \in \left[ {0;\,2017} \right]\end{array} \right.\)\( \Rightarrow m \in \left\{ {0;10;\,11;\,12;\,...;\,2017} \right\}\)
Vậy có \(2009\) giá trị nguyên của \(m\) thỏa mãn.
Tìm \(m\) để phương trình \({x^2} - mx + {m^2} - 3 = 0\) có hai nghiệm \({x_1}\), \({x_2}\) là độ dài các cạnh góc vuông của một tam giác vuông với cạnh huyền có độ dài bằng \(2\) là
Phương trình \({x^2} - mx + {m^2} - 3 = 0\) có hai nghiệm \({x_1}\), \({x_2}\) là độ dài các cạnh góc vuông của một tam giác với cạnh huyền có độ bài bằng \(2\) khi và chỉ khi:
\(\left\{ \begin{array}{l}\Delta = {m^2} - 4{m^2} + 12 \ge 0\\S = {x_1} + {x_2} = m > 0\\P = {x_1}.{x_2} > 0\\x_1^2 + x_2^2 = 4\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}3 < {m^2} \le 4\\m > 0\\{\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\sqrt 3 < m \le 2\\{m^2} - 2\left( {{m^2} - 3} \right) = 4\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}\sqrt 3 < m \le 2\\{m^2} = 2\end{array} \right.\) \( \Leftrightarrow m \in \emptyset \)
Tất cả các giá trị của tham số \(m\) để phương trình $\left( {{x^2} + \dfrac{1}{{{x^2}}}} \right) - 2m\left( {x + \dfrac{1}{x}} \right) + 1 = 0$ có nghiệm là
Ta có $\left( {{x^2} + \dfrac{1}{{{x^2}}}} \right) - 2m\left( {x + \dfrac{1}{x}} \right) + 1 = 0$\( \Leftrightarrow {\left( {x + \dfrac{1}{x}} \right)^2} - 2m\left( {x + \dfrac{1}{x}} \right) - 1 = 0\) (1)
Đặt \(x + \dfrac{1}{x} = t\), \(\left| t \right| \ge 2\) ta được \({t^2} - 2mt - 1 = 0\) (2).
Phương trình (2) luôn có hai nghiệm \({t_1} < 0 < {t_2}\) (do \(a.c = - 1 < 0\) )\( \Rightarrow \) phương trình (1) có nghiệm khi và chỉ khi phương trình (2) có ít nhất một nghiệm \(t\) sao cho \(\left| t \right| \ge 2\), hay ít nhất một trong hai số \(2;\,\, - 2\) phải nằm giữa hai nghiệm \({t_1},\,\,{t_2};\) hay \(\left[ \begin{array}{l}f\left( 2 \right) \le 0\\f\left( { - 2} \right) \le 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}3 - 4m \le 0\\3 + 4m \le 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}m \ge \dfrac{3}{4}\\m \le - \dfrac{3}{4}\end{array} \right.\).
Tìm tất cả các giá trị thực của \(m\) để phương trình \({x^2} - 4x + 6 + 3m = 0\) có nghiệm thuộc đoạn \(\left[ { - 1;3} \right]\).
Ta có: \({x^2} - 4x + 6 + 3m = 0\) \( \Leftrightarrow 3m = - {x^2} + 4x - 6\).
Số nghiệm của phương trình \({x^2} - 4x + 6 + 3m = 0\) là số giao điểm của đường thẳng \(y = 3m\) và parabol \(y = - {x^2} + 4x - 6\).
Parabol \(y = - {x^2} + 4x - 6\) có hoành độ đỉnh $x=2\in \left[ { - 1;3} \right]$, hệ số $a=-1<0$ nên đồng biến khi $x<2$ và nghịch biến khi $x>2$.
Bảng biến thiên của hàm số \(y = - {x^2} + 4x - 6\) trên đoạn \(\left[ { - 1;3} \right]\):
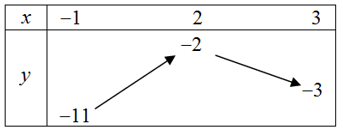
Từ bảng biến thiên ta thấy, nếu phương trình có nghiệm trên đoạn $[-1;3]$ thì đường thẳng $y=3m$ phải cắt parabol tại ít nhất $1$ điểm có hoành độ thuộc đoạn $[-1;3]$.
Phương trình có nghiệm thuộc đoạn \(\left[ { - 1;3} \right]\)\( \Leftrightarrow - 11 \le 3m \le - 2\)\( \Leftrightarrow - \dfrac{{11}}{3} \le m \le - \dfrac{2}{3}\).
Xác định $m$ để phương trình \(m = \left| {{x^2} - 6x - 7} \right|\) có $4$ nghiệm phân biệt.
\(m = \left| {{x^2} - 6x - 7} \right|\) là phương trình hoành độ giao điểm của đường thẳng \(y = m\) và đồ thị \(\left( C \right):\,\,y = \left| {{x^2} - 6x - 7} \right|\).
Vẽ \(\left( P \right):\,\,y = {x^2} - 6x - 7\), lấy đối xứng phần phía dưới \(Ox\) của \(\left( P \right)\) lên trên \(Ox\) và xóa đi phần phía dưới \(Ox\) (vì \(y = \left| {{x^2} - 6x - 7} \right| \ge 0,\,\forall x \in \mathbb{R}\)), ta được đồ thị \(\left( C \right)\).
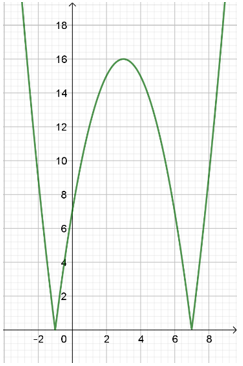
Dựa vào đồ thị: phương trình \(m = \left| {{x^2} - 6x - 7} \right|\) có 4 nghiệm phân biệt khi \(m \in \left( {0;16} \right)\).
Hệ phương trình \(\left\{ \begin{array}{l}{x^2} = 3x - y\\{y^2} = 3y - x\end{array} \right.\) có bao nhiêu nghiệm?
\(\left\{ \begin{array}{l}{x^2} = 3x - y{\rm{ }}\,\left( 1 \right)\\{y^2} = 3y - x\,{\rm{ }}\left( 2 \right)\end{array} \right.\).
Lấy $\left( 1 \right)$ trừ $\left( 2 \right)$ theo vế ta được: \({x^2} - {y^2} = 4x - 4y\)\( \Leftrightarrow \left( {x - y} \right)\left( {x + y - 4} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}y = x\\y = 4 - x\end{array} \right.\).
TH1: \(\left\{ \begin{array}{l}{x^2} = 3x - y\,\\y = x\end{array} \right.\)$ \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 2x = 0\,\\y = x\end{array} \right.$$ \Leftrightarrow \left[ \begin{array}{l}x = y = 0\\x = y = 2\end{array} \right.$.
TH2: \(\left\{ \begin{array}{l}{x^2} = 3x - y\,\\y = 4 - x\end{array} \right.\)$ \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 4x + 4 = 0\,\\y = 4 - x\end{array} \right.$$ \Leftrightarrow x = y = 2$.
Vậy hệ có hai nghiệm.
Có bao nhiêu giá trị $m$ nguyên để phương trình \(\sqrt {x + 2} + \sqrt {2 - x} + 2\sqrt { - {x^2} + 4} - 2m + 3 = 0\) có nghiệm.
Đặt \(t = \sqrt {x + 2} + \sqrt {2 - x} \)
Điều kiện \(t = \sqrt {x + 2} + \sqrt {2 - x} \ge \sqrt {x + 2 + 2 - x} = 2 \Rightarrow t \ge 2\)
Lại có \(\sqrt {x + 2} + \sqrt {2 - x} \le \sqrt {{1^2} + {1^2}} .\sqrt {x + 2 + 2 - x} = 2\sqrt 2 \) \( \Rightarrow t \le 2\sqrt 2 \)
Suy ra \(2 \le t \le 2\sqrt 2 \)
Ta có: \({t^2} = 4 + 2\sqrt {4 - {x^2}} \)\( \Rightarrow 2\sqrt {4 - {x^2}} = {t^2} - 4\)
Phương trình trở thành: \(t + {t^2} - 4 - 2m + 3 = 0\)\( \Leftrightarrow {t^2} + t - 2m - 1 = 0\)\( \Leftrightarrow {t^2} + t - 1 = 2m\,\,\,(*)\)
Xét hàm số \(f\left( t \right) = {t^2} + t - 1\) (parabol có hoành độ đỉnh \(x = - \dfrac{1}{2} \notin \left[ {2;2\sqrt 2 } \right]\)) trên \(\left[ {2;2\sqrt 2 } \right]\), có bảng biến thiên
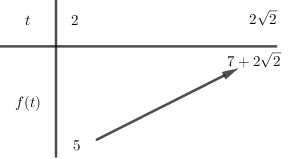
Phương trình $(*)$ có nghiệm thỏa \(2 \le t \le 2\sqrt 2 \) khi \(5 \le 2m \le 7 + 2\sqrt 2 \)\( \Rightarrow \dfrac{5}{2} \le m \le \dfrac{{7 + 2\sqrt 2 }}{2}\)
\(\dfrac{5}{2} \le m \le \dfrac{{7 + 2\sqrt 2 }}{2}\,\)\( \to \left( {2,5 \le m \le 4,91} \right)\)
Vậy có 2 giá trị \(m\) nguyên dương là \(m = 3\), \(m = 4\).
Cho phương trình \(m{x^2} + \left( {{m^2} - 3} \right)x + m = 0\). Tìm tất cả các giá trị của tham số \(m\) để phương trình có hai nghiệm \({x_1}\), \({x_2}\) thỏa mãn \({x_1} + {x_2} = \dfrac{{13}}{4}\). Khi đó tổng bình phương các giá trị tìm được của tham số \(m\) bằng
Phương trình có \(2\) nghiệm \({x_1}\), \({x_2}\) thỏa mãn \({x_1} + {x_2} = \dfrac{{13}}{4}\)
\( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta \ge 0\\ - \dfrac{b}{a} = \dfrac{{13}}{4}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\{\left( {{m^2} - 3} \right)^2} - 4{m^2} \ge 0\\ - \dfrac{{{m^2} - 3}}{m} = \dfrac{{13}}{4}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\left( {{m^2} - 3 - 2m} \right)\left( {{m^2} - 3 + 2m} \right) \ge 0\\4{m^2} + 13m - 12 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\left( {m + 1} \right)\left( {m - 3} \right)\left( {m - 1} \right)\left( {m + 3} \right) \ge 0\\m = \dfrac{3}{4};m = - 4\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \in \left( { - \infty ; - 3} \right] \cup \left[ { - 1;1} \right] \cup \left[ {3; + \infty } \right)\\m = \dfrac{3}{4};m = - 4\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{3}{4}\\m = - 4\end{array} \right.\).
Vậy tổng bình phương các giá trị của \(m\) là \(\dfrac{{265}}{{16}}\).
Một số tự nhiên có hai chữ số có dạng \(\overline {ab} \), biết hiệu của hai chữ số đó bằng \(3\). Nếu viết các chữ số theo thứ tự ngược lại thì được một số bằng \(\dfrac{4}{5}\) số ban đầu trừ đi \(10\). Khi đó \({a^2} + {b^2}\) bằng
Ta có: \(|a - b| = 3\) \(\left( {a,b \in \mathbb{N}} \right)\).
Khi viết ngược lại ta có:$10b + a = \dfrac{4}{5}\left( {10a + b} \right) - 10$$ \Leftrightarrow 35a - 46b = 50$.
Xét hệ phương trình: \(\left\{ \begin{array}{l}a - b = 3\\35a - 46b = 50\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 8\\b = 5\end{array} \right.\).
Hoặc \(\left\{ \begin{array}{l} - a + b = 3\\35a - 46b = 50\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{{188}}{{11}}\\b = - \dfrac{{155}}{{11}}\end{array} \right.\) (loại).
Với \(a = 8\), \(b = 5\), \({a^2} + {b^2} = 89\).
Có bao nhiêu giá trị nguyên của m để phương trình \({x^2} - 4\sqrt {{x^2} + 1} - \left( {m - 1} \right) = 0\) có \(4\) nghiệm phân biệt
Điều kiện xác định \(x \in \mathbb{R}\).
Đặt \(t = \sqrt {{x^2} + 1} \), \(t \ge 1\).
Phương trình trở thành \({t^2} - 1 - 4t - m + 1 = 0\)\( \Leftrightarrow {t^2} - 4t = m\). \(\left( 2 \right)\)
Để phương trình có \(4\) nghiệm phân biệt thì phương trình \(\left( 2 \right)\) có hai nghiệm phân biệt lớn hơn \(1\).
Xét hàm số \(f\left( t \right) = {t^2} - 4t\) có đồ thị là parabol có hoành độ đỉnh \(x = 2 \in \left( {1; + \infty } \right)\) nên ta có bảng biến thiên:
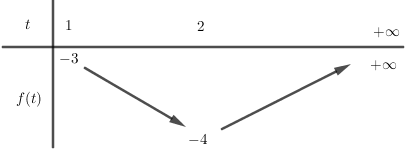
Dựa BBT ta thấy để $(2)$ có hai nghiệm phân biệt lớn hơn $1$ thì \( - 4 < m < - 3\).
Vậy không có giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.
Tập tất cả các giá trị của tham số \(m\) để phương trình \({x^2} - 2mx + m + 2 = 0\) có hai nghiệm dương phân biệt là
Để phương trình \({x^2} - 2mx + m + 2 = 0\) có hai nghiệm dương phân biệt
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\S > 0\\P > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{\left( { - m} \right)^2} - 1.\left( {m + 2} \right) > 0\\2m > 0\\m + 2 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - m - 2 > 0\\m > 0\\m > - 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m < - 1,m > 2\\m > 0\\m > - 2\end{array} \right.\)\( \Leftrightarrow m > 2\).
Vậy: $m > 2$.
Biết phương trình \(3x + 1 - \sqrt {3{x^2} + 7x} - \sqrt {3x - 1} = 0\) có một nghiệm có dạng \(x = \dfrac{{a + \sqrt b }}{c}\), trong đó \(a\), \(b\), \(c\) là các số nguyên tố. Tính \(S = a + b + c\).
Điều kiện: \(\left\{ \begin{array}{l}3{x^2} + 7x \ge 0\\3x - 1 \ge 0\end{array} \right. \Leftrightarrow x \ge \dfrac{1}{3}\;\left( * \right)\)
Với điều kiện trên, phương trình tương đương
\(\left[ {\left( {2x + 1} \right) - \sqrt {3{x^2} + 7x} } \right] + \left[ {x - \sqrt {3x - 1} } \right] = 0\)
\( \Leftrightarrow \dfrac{{{x^2} - 3x + 1}}{{\left( {2x + 1} \right) + \sqrt {3{x^2} + 7x} }} + \dfrac{{{x^2} - 3x + 1}}{{x + \sqrt {3x - 1} }} = 0\)
\( \Leftrightarrow \left( {{x^2} - 3x + 1} \right)\left( {\dfrac{1}{{2x + 1 + \sqrt {3{x^2} + 7x} }} + \dfrac{1}{{x + \sqrt {3x - 1} }}} \right) = 0\)
\( \Leftrightarrow {x^2} - 3x + 1 = 0\) (do \(\left( * \right)\) \( \Rightarrow \dfrac{1}{{2x + 1 + \sqrt {3{x^2} + 7x} }} + \dfrac{1}{{x + \sqrt {3x - 1} }} > 0\))
\( \Leftrightarrow x = \dfrac{{3 + \sqrt 5 }}{2}\) hoặc \(x = \dfrac{{3 - \sqrt 5 }}{2}\)
Theo yêu cầu đề bài ta chọn nghiệm \(x = \dfrac{{3 + \sqrt 5 }}{2}\)
Vậy \(a = 3\), \(b = 5\), \(c = 2\) \( \Rightarrow S = a + b + c = 10\).
Hệ phương trình \(\left\{ \begin{array}{l}{\left( {2x + y} \right)^2} - 5\left( {4{x^2} - {y^2}} \right) + 6\left( {4{x^2} - 4xy + {y^2}} \right) = 0\\2x + y + \dfrac{1}{{2x - y}} = 3\end{array} \right.\) có một nghiệm \(\left( {{x_0}; {y_0}} \right)\) thỏa mãn \({x_0} > \dfrac{1}{2}\). Khi đó \(P = {x_0} + y_0^2\) có giá trị là
Ta có \(\left\{ \begin{array}{l}{\left( {2x + y} \right)^2} - 5\left( {4{x^2} - {y^2}} \right) + 6\left( {4{x^2} - 4xy + {y^2}} \right) = 0 \left( 1 \right)\\2x + y + \dfrac{1}{{2x - y}} = 3 \left( 2 \right)\end{array} \right.\).
\(\left( 1 \right) \Leftrightarrow 8{x^2} + 12{y^2} - 20xy = 0\) \( \Leftrightarrow \left( {x - y} \right)\left( {2x - 3y} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = y\\2x = 3y\end{array} \right.\).
Với \(x = y\) ta có \(\left( 2 \right) \Rightarrow 3x + \dfrac{1}{x} = 3\) \( \Leftrightarrow 3{x^2} - 3x + 1 = 0\): phương trình vô nghiệm.
Với \(2x = 3y\) ta có \(\left( 2 \right) \Rightarrow 4y + \dfrac{1}{{2y}} = 3\) \( \Leftrightarrow 8{y^2} - 6y + 1 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}y = \dfrac{1}{2}\\y = \dfrac{1}{4}\end{array} \right.\).
Với \(y = \dfrac{1}{4}\) \( \Rightarrow x = \dfrac{3}{8}\left( {KTM} \right)\).
Với \(y = \dfrac{1}{2}\) \( \Rightarrow x = \dfrac{3}{4}\left( {TM} \right)\)\( \Rightarrow P = 1\).
Cho hàm số $y = - {x^2} + 4x - 3$, có đồ thị $\left( P \right)$. Giả sử $d$ là dường thẳng đi qua $A\left( {0;\, - 3} \right)$ và có hệ số góc $k$. Xác định $k$ sao cho $d$ cắt đồ thị $\left( P \right)$ tại $2$ điểm phân biệt $E$, $F$ sao cho $\Delta OEF$ vuông tại $O$ ($O$ là gốc tọa độ). Khi đó
Phương trình đường thẳng $d:y = kx - 3$
Phương trình hoành độ giao điểm của $\left( P \right)$ và $d$: $ - {x^2} + 4x - 3 = kx - 3$ $ \Leftrightarrow - {x^2} + \left( {4 - k} \right)x = 0$ $ \Leftrightarrow x\left( { - x + 4 - k} \right) = 0$ $\,\left( 1 \right)$
$d$ cắt đồ thị $\left( P \right)$ tại $2$ điểm phân biệt khi $\,\left( 1 \right)$ có $2$ nghiệm phân biệt$ \Leftrightarrow 4 - k \ne 0$$ \Leftrightarrow k \ne 4$.
Ta có $E\left( {{x_1};\,k{x_1} - 3} \right)$, $F\left( {{x_2};\,k{x_2} - 3} \right)$ với ${x_1}$, ${x_2}$ là nghiệm phương trình $\left( 1 \right)$
$\Delta OEF$ vuông tại $O$$ \Rightarrow \overrightarrow {OE} .\overrightarrow {OF} = 0$$ \Leftrightarrow {x_1}.{x_2} + \left( {k{x_1} - 3} \right)\left( {k{x_2} - 3} \right) = 0$$ \Leftrightarrow {x_1}.{x_2}\left( {1 + {k^2}} \right) - 3k\left( {{x_1} + {x_2}} \right) + 9 = 0$$ \Leftrightarrow 0.\left( {1 + {k^2}} \right) - 3k\left( {4 - k} \right) + 9 = 0$
$ \Leftrightarrow {k^2} - 4k + 3 = 0$$ \Leftrightarrow \left[ \begin{array}{l}k = 1\\k = 3\end{array} \right.$
Để phương trình sau có \(4\) nghiệm phân biệt: \(\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\). Giá trị của tham số \(a\) là
Phương trình đã cho tương đương: \(2\left| {{x^2} - 5x + 4} \right| = {x^2} - 5x + a\), \(\left( 1 \right)\).
Đặt \(t = {x^2} - 5x + a\).
Phương trình \(\left( 1 \right)\) trở thành: \(2\left| {t + 4 - a} \right| = t\), \(\left( 2 \right)\)
Phương trình \(\left( 2 \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}t \ge 0\\\left[ \begin{array}{l}t = 2a - 8\\t = \dfrac{{2a - 8}}{3}\end{array} \right.\end{array} \right.\), để phương trình \(\left( 1 \right)\) có \(4\) nghiệm phân biệt thì điều kiện cần là \(\left( 2 \right)\) phải có \(2\) nghiệm phân biệt, tức là \(2a - 8 > 0\)\( \Leftrightarrow a > 4\), \(\left( * \right)\).
Khi đó, thay lại ta có: \(\left[ \begin{array}{l}{x^2} - 5x + a = 2a - 8\\3{x^2} - 15x + 3a = 2a - 8\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}{x^2} - 5x + 8 - a = 0\,\,\,\,\left( 3 \right)\\3{x^2} - 15x + a + 8 = 0\,\,\,\left( 4 \right)\end{array} \right.\).
Điều kiện để \(\left( 1 \right)\) có \(4\) nghiệm phân biệt là mỗi phương trình bậc \(2\) ở trên có \(2\) nghiệm phân biệt và hai nghiệm của \(\left( 3 \right)\) không thỏa mãn \(\left( 4 \right)\)
Mỗi phương trình \(\left( 3 \right),\left( 4 \right)\) có hai nghiệm phân biệt khi và chỉ khi
\(\left\{ \begin{array}{l}{\Delta _1} = 25 - 4\left( {8 - a} \right) > 0\\{\Delta _2} = {15^2} - 4.3.\left( {a + 8} \right) > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a > \dfrac{7}{4}\\a < \dfrac{{43}}{4}\end{array} \right.\)\( \Leftrightarrow \dfrac{7}{4} < a < \dfrac{{43}}{4}\).
Nếu \(x\) là nghiệm của \(\left( 3 \right)\) thì không thỏa mãn \(\left( 4 \right)\)
\( \Rightarrow \left\{ \begin{array}{l}{x^2} - 5x + 8 - a = 0\\3{x^2} - 15x + a + 8 \ne 0\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x^2} - 5x + 8 - a = 0\\3\left( {{x^2} - 5x + 8 - a} \right) - 16 + 4a \ne 0\end{array} \right.\)\( \Rightarrow 4a - 16 \ne 0 \Leftrightarrow a \ne 4\)
So với điều kiện \(\left( * \right)\), suy ra \(4 < a < \dfrac{{43}}{4}\).
