Tìm tất cả các giá trị thực của \(m\) để phương trình \({x^2} - 4x + 6 + 3m = 0\) có nghiệm thuộc đoạn \(\left[ { - 1;3} \right]\).

Ta có: \({x^2} - 4x + 6 + 3m = 0\) \( \Leftrightarrow 3m =  - {x^2} + 4x - 6\).

Số nghiệm của phương trình \({x^2} - 4x + 6 + 3m = 0\) là số giao điểm của đường thẳng \(y = 3m\) và parabol \(y =  - {x^2} + 4x - 6\).

Parabol \(y =  - {x^2} + 4x - 6\) có hoành độ đỉnh $x=2\in \left[ { - 1;3} \right]$, hệ số $a=-1<0$ nên đồng biến khi $x<2$ và nghịch biến khi $x>2$.

Bảng biến thiên của hàm số \(y =  - {x^2} + 4x - 6\) trên đoạn \(\left[ { - 1;3} \right]\):

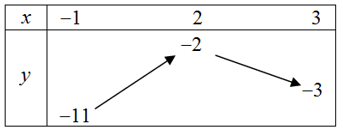
Từ bảng biến thiên ta thấy, nếu phương trình có nghiệm trên đoạn $[-1;3]$ thì đường thẳng $y=3m$ phải cắt parabol tại ít nhất $1$ điểm có hoành độ thuộc đoạn $[-1;3]$.

Phương trình có nghiệm thuộc đoạn \(\left[ { - 1;3} \right]\)\( \Leftrightarrow  - 11 \le 3m \le  - 2\)\( \Leftrightarrow  - \dfrac{{11}}{3} \le m \le  - \dfrac{2}{3}\).