Xác định $m$ để phương trình \(m = \left| {{x^2} - 6x - 7} \right|\) có $4$ nghiệm phân biệt.
Trả lời bởi giáo viên
\(m = \left| {{x^2} - 6x - 7} \right|\) là phương trình hoành độ giao điểm của đường thẳng \(y = m\) và đồ thị \(\left( C \right):\,\,y = \left| {{x^2} - 6x - 7} \right|\).
Vẽ \(\left( P \right):\,\,y = {x^2} - 6x - 7\), lấy đối xứng phần phía dưới \(Ox\) của \(\left( P \right)\) lên trên \(Ox\) và xóa đi phần phía dưới \(Ox\) (vì \(y = \left| {{x^2} - 6x - 7} \right| \ge 0,\,\forall x \in \mathbb{R}\)), ta được đồ thị \(\left( C \right)\).
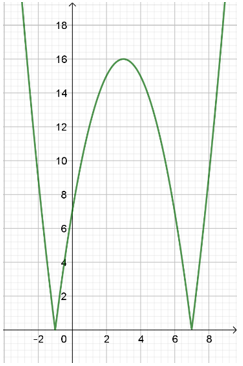
Dựa vào đồ thị: phương trình \(m = \left| {{x^2} - 6x - 7} \right|\) có 4 nghiệm phân biệt khi \(m \in \left( {0;16} \right)\).
Hướng dẫn giải:
- Dựng đồ thị hàm số \(y = \left| {{x^2} - 6x - 7} \right|\) từ đồ thị hàm số \(y = {x^2} - 6x - 7\)
- Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số trên và đường thẳng \(y = m\)

