Trong một khoảng thời gian nhất định, tại một địa phương, Đài khí tượng thủy văn đã thống kê được: Số ngày mưa: 10 ngày; Số ngày có gió: 8 ngày; Số ngày lạnh: 6 ngày; Số ngày mưa và gió: 5 ngày; Số ngày mưa và lạnh : 4 ngày; Số ngày lạnh và có gió: 3 ngày; Số ngày mưa, lạnh và có gió: 1 ngày. Vậy có bao nhiêu ngày thời tiết xấu (Có gió, mưa hay lạnh)?
Ký hiệu A là tập hợp những ngày mưa, B là tập hợp những ngày có gió, C là tập hợp những ngày lạnh.
Theo giả thiết ta có:\(n\left( A \right) = 10,{\rm{ }}n\left( B \right) = 8\) , \(n\left( C \right) = 6,\)
\(n(A \cap B) = {\rm{ }}5,{\rm{ }}n(A \cap C) = 4,{\rm{ }}n(B \cap C) = 3,\,\,n(A \cap B \cap C) = 1\)
Để tìm số ngày thời tiết xấu ta sử dụng biểu đồ Ven(hình vẽ). Ta cần tính \(n(A \cup B \cup C)\).
Xét tổng \(n\left( A \right) + n\left( B \right) + n\left( C \right)\): trong tổng này, mỗi phần tử của A giao B, B giao C, C giao A được tính làm hai lần nên trong tổng \(n\left( A \right) + n\left( B \right) + n\left( C \right)\) ta phải trừ đi tổng \(n(A \cap B) + n(B \cap C) + n(C \cap A)\).
Trong tổng \(n\left( A \right) + n\left( B \right) + n\left( C \right)\) được tính \(n\left( {A \cap B \cap C} \right)\) 3 lần, trong \(n(A \cap B) + n(B \cap C) + n(C \cap A)\) cũng được tính \(n\left( {A \cap B \cap C} \right)\) 3 lần. Vì vậy
\(\begin{array}{l}n(A \cup B \cup C) = n\left( A \right) + n\left( B \right) + n\left( C \right) \\- n(A \cap B) - n(B \cap C) - n(C \cap A) \\+ n\left( {A \cap B \cap C} \right)\\ = 10 + 8 + 6 - (5 + 4 + 3) + 1 = 13.\end{array}\)
Vậy số ngày thời tiết xấu là \(13\) ngày.
Lớp 10A có \(10\) học sinh giỏi Toán, \(10\) học sinh giỏi Lý, \(11\) học sinh giỏi Hóa, \(6\) học sinh giỏi cả Toán và Lý, \(5\) học sinh giỏi cả Hóa và Lý, \(4\) học sinh giỏi cả Toán và Hóa, \(3\) học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là
Theo giả thiết đề bài cho, ta có biểu đồ Ven:
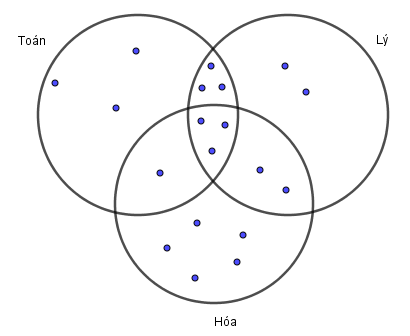
Dựa vào biểu đồ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: \(6 - 3 = 3\) (em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: \(4 - 3 = 1\) (em)
Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là: \(5 - 3 = 2\) (em)
Số học sinh chỉ giỏi một môn Toán là: \(10 - 3 - 3 - 1 = 3\) (em)
Số học sinh chỉ giỏi một môn Lý là: \(10 - 3 - 3 - 2 = 2\) (em)
Số học sinh chỉ giỏi một môn Hóa là: \(11 - 1 - 3 - 2 = 5\) (em)
Số học sinh giỏi ít nhất một trong ba môn là:
\(3 + 2 + 5 + 1 + 2 + 3 + 3 = 19\) (em)
Cho các tập hợp khác rỗng \(A=\left[ {m - 1;\dfrac{{m + 3}}{2}} \right]\) và \(B = \left( { - \infty ; - 3} \right) \cup \left[ {3; + \infty } \right)\). Tập hợp các giá trị thực của \(m\) để \(A \cap B \ne \emptyset \) là
Để \(A \cap B \ne \emptyset \) thì điều kiện là \(\left\{ \begin{array}{l}m - 1 \le \dfrac{{m + 3}}{2}\\\left[ \begin{array}{l}m - 1 < - 3\\\dfrac{{m + 3}}{2} \ge 3\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 5\\\left[ \begin{array}{l}m < - 2\\m \ge 3\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m \le 5\\m < - 2\end{array} \right.\\\left\{ \begin{array}{l}m \le 5\\m \ge 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < - 2\\3 \le m \le 5\end{array} \right.\).
Vậy \(m \in \left( { - \infty - 2} \right) \cup \left[ {3;5} \right]\)
Minh họa bằng trục số
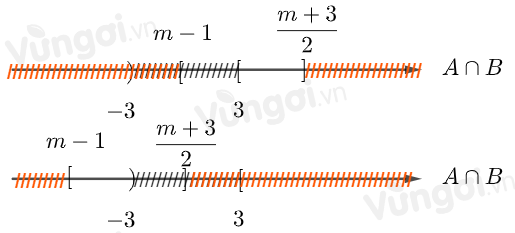
Cho các tập hợp khác rỗng $A = \left( { - \infty ;\,m} \right)$ và $B = \left[ {2m - 2;\,2m + 2} \right]$. Tìm $m \in \mathbb{R}$ để $({C_{\mathbb{R}}}A) \cap B \ne \emptyset $.
Ta có: $C_{\mathbb{R}}A = \left[ {m;\, + \infty } \right)$.
Để $C_{\mathbb{R}}A \cap B \ne \emptyset \Leftrightarrow 2m + 2 \ge m \Leftrightarrow m \ge - 2$.
Trong các mệnh đề sau, mệnh đề nào sai?
+ Xét đáp án A. Khi $n = 3$ thì giá trị của $\left( {{n^2} + 11n + 2} \right)$ bằng $44 \vdots 11$ nên đáp án A đúng
+ Xét đáp án B. Khi $n = 2k,\,k \in N \Rightarrow {n^2} + 1 = 4{k^2} + 1$ không chia hết cho $4$, $k \in N$.
Khi $n = 2k + 1,\,k \in N \Rightarrow {n^2} + 1 = {\left( {2k + 1} \right)^2} + 1 = 4{k^2} + 4k + 2$ không chia hết cho $4$, $k \in N$.
+ Xét đáp án C. Tồn tại số nguyên tố $5$ chia hết cho $5$ nên đáp án C đúng
+ Xét đáp án D. Phương trình $2{x^2} - 8 = 0 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = - 2;\,\,x = 2 \in Z$ nên đáp án D đúng.
Cho \(A = \left( {2; + \infty } \right)\), \(B = \left( {m; + \infty } \right)\). Điều kiện cần và đủ của $m$ sao cho $B$ là tập con của $A$ là

Ta có: \(B \subset A\) khi và chỉ khi $\left( {m; + \infty } \right)\subset \left( {2; + \infty } \right)$, do đó \(\forall x \in B \Rightarrow x \in A\)\( \Rightarrow m \ge 2\).
Trong các mệnh đề sau, mệnh đề nào đúng?
A sai vì với \(x = 1\) thì \({\left( {x - 1} \right)^2} = x - 1\).
B sai vì khi \(x = - 4 < 3\) nhưng \(\left| x \right| = 4 > 3\).
C sai vì
+ Nếu \(n = 2k\,\,\left( {k \in \mathbb{N}} \right)\) thì \({n^2} + 1 = 4{k^2} + 1\) số này không chia hết cho \(4\).
+ Nếu \(n = 2k + 1\,\,\left( {k \in \mathbb{N}} \right)\) thì \({n^2} + 1 = 4{k^2} + 4k + 2\) số này cũng không chia hết cho $4$.
D đúng vì
+ Nếu \(n = 3k\,\,\left( {k \in \mathbb{N}} \right)\) thì \({n^2} + 1 = 9{k^2} + 1\) số này không chia hết cho \(3\).
+ Nếu \(n = 3k \pm 1\,\,\left( {k \in {\mathbb{N}^*}} \right) \) thì \({n^2} + 1 = 9{k^2} \pm 6k + 2\) số này không chia hết cho \(3\).
Cho ba tập hợp:
\(M\): tập hợp các tam giác có \(2\) góc tù.
\(N\): tập hợp các tam giác có độ dài ba cạnh là ba số nguyên liên tiếp.
\(P\): tập hợp các số nguyên tố chia hết cho \(3\).
Tập hợp nào là tập hợp rỗng?
\(M{\rm{ }} = {\rm{ }}\emptyset \)
Tổng ba góc trong tam giác bằng \(180^\circ \) nên không thể có hai góc tù.
\(N \ne \emptyset \) vì nó chứa tam giác có $3$ cạnh là $3;4;5$ và nhiều tam giác khác.
Có thể chứng minh được nếu số nhỏ nhất trong $3$ số tự nhiên liên tiếp lớn hơn $1$ thì ba số tự nhiên liên tiếp đó luôn có thể là $3$ cạnh của tam giác.
Số nguyên tố chia hết cho \(3\) là số \(3\).
\(P = \left\{ 3 \right\}\).
Xác định số phần tử của tập hợp \(X = \left\{ {n \in \mathbb{N}|n\, \vdots \,4\,,\,n < 2017} \right\}\).
Các số tự nhiên chia hết cho \(4\) nhỏ hơn \(2017\) là \(0;4;8;...;2016\)
Số phần tử của tập hợp \(X\) là: \(\left( {2016 - 0} \right):4 + 1 = 505\) (số)
Vậy có tất cả $505$ số tự nhiên nhỏ hơn $2017$ và chia hết cho $4$.
Cho hai tập hợp \(A = \left[ {1;3} \right]\) và \(B = \left[ {m;m + 1} \right]\). Tìm tất cả giá trị của tham số \(m\) để \(B \subset A\).
Ta có: \(B \subset A \Leftrightarrow 1 \leqslant m \leqslant m + 1 \leqslant 3 \Leftrightarrow\left\{ \begin{array}{l}m \ge 1\\m + 1 \le 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge 1\\m \le 2\end{array} \right.\)
Vậy \(1 \le m \le 2\).
Cho \(m\) là một tham số thực và hai tập hợp khác rỗng \(A = \left[ {1 - 2m;\,m + 3} \right]\), \(B = \left\{ {x \in \mathbb{R}|\,x \ge 8 - 5m} \right\}\). Tất cả các giá trị \(m\) để \(A \cap B = \emptyset \) là
Ta có \(A = \left[ {1 - 2m;\,m + 3} \right]\), \(B = \left[ {8 - 5m;\, + \infty } \right)\).
\(A \cap B = \emptyset \) \( \Leftrightarrow \left\{ \begin{array}{l}m + 3 < 8 - 5m\\1 - 2m \le m + 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}6m < 5\\3m \ge - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m < \dfrac{5}{6}\\m \ge - \dfrac{2}{3}\end{array} \right.\) \( \Leftrightarrow - \dfrac{2}{3} \le m < \dfrac{5}{6}\)
Lớp \(10A\) có \(7\) học sinh giỏi Toán, \(5\) học sinh giỏi Lý, \(6\) học sinh giỏi Hoá, \(3\) học sinh giỏi cả Toán và Lý, \(4\) học sinh giỏi cả Toán và Hoá, \(2\) học sinh giỏi cả Lý và Hoá, \(1\) học sinh giỏi cả ba môn Toán, Lý, Hoá. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hoá ) của lớp \(10A\) là
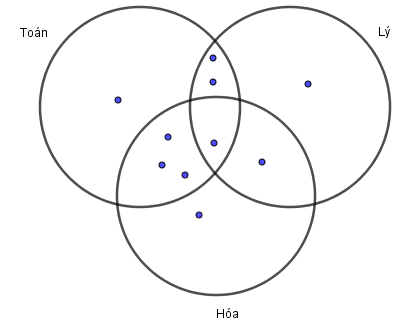
Số học sinh giỏi toán, lý mà không giỏi hóa: \(3 - 1 = 2\).
Số học sinh giỏi toán, hóa mà không giỏi lý: \(4 - 1 = 3\).
Số học sinh giỏi hóa, lý mà không giỏi toán: \(2 - 1 = 1\).
Số học sinh chỉ giỏi môn lý: \(5 - 2 - 1 - 1 = 1\).
Số học sinh chỉ giỏi môn hóa: \(6 - 3 - 1 - 1 = 1\).
Số học sinh chỉ giỏi môn toán: \(7 - 3 - 2 - 1 = 1\).
Số học sinh giỏi ít nhất một (môn toán, lý, hóa) là số học sinh giỏi \(1\) môn hoặc \(2\) môn hoặc cả \(3\) môn: \(1 + 1 + 1 + 1 + 2 + 3 + 1 = 10\).
Cho \(A = \left\{ {x \in \mathbb{R}\,\,\left| {\left| {mx - 3} \right| = mx - 3} \right.} \right\}\), \(B = \left\{ {x \in \mathbb{R}\,\,\left| {{x^2} - 4 = 0} \right.} \right\}\). Tìm \(m\) để \(B\backslash A = B\).
Ta có: \(x \in A \Leftrightarrow mx - 3 \ge 0\).
+ Nếu \(m = 0\) thì \( - 3 \ge 0\) (vô lý) nên \(A = \emptyset \)
+ Nếu \(m > 0\) thì \(x \ge \dfrac{3}{m}\) hay \(A = \left[ {\dfrac{3}{m}; + \infty } \right)\)
+ Nếu \(m < 0\) thì \(x \le \dfrac{3}{m}\) hay \(A = \left( { - \infty ;\dfrac{3}{m}} \right]\)
\(x \in B \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 2}\\{x = - 2}\end{array}} \right.\) hay \(B = \left\{ { - 2;2} \right\}\)
Ta có: $B\backslash A = B \Leftrightarrow B \cap A = \emptyset $$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}\begin{array}{l}m = 0\\\left\{ {\begin{array}{*{20}{c}}{m > 0}\\{\dfrac{3}{m} > 2}\end{array}} \right.\end{array}\\{\left\{ {\begin{array}{*{20}{c}}{m < 0}\\{\dfrac{3}{m} < - 2}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}\begin{array}{l}m = 0\\0 < m < \dfrac{3}{2}\end{array}\\{ - \dfrac{3}{2} < m < 0}\end{array}} \right.$ $ \Leftrightarrow - \dfrac{3}{2} < m < \dfrac{3}{2}$
Liệt kê các phần tử của tập hợp \(B = \left\{ {\left. {x \in \mathbb{Z}} \right|\dfrac{{3{x^2} + 2x + 2}}{{x + 1}} \in \mathbb{Z}} \right\}\).
\(\dfrac{{3{x^2} + 2x + 2}}{{x + 1}} = 3x - 1 + \dfrac{3}{{x + 1}}\)
Điều kiện: \(x + 1 \ne 0 \Leftrightarrow x \ne - 1.\)
Vì \(x \in \mathbb{Z}\) nên \(x + 1 \in \mathbb{Z}\).
Để \(\dfrac{{3{x^2} + 2x + 2}}{{x + 1}} \in \mathbb{Z}\) thì \(\dfrac{3}{{x + 1}} \in \mathbb{Z} \Rightarrow \left( {x + 1} \right) \in U\left( 3 \right) = \left\{ { \pm 1;\,\, \pm 3} \right\}.\)
Ta có bảng sau:
Vậy \(B = \left\{ { - 4;\,\, - 2;\,\,0;\,\,2} \right\}\).