Câu hỏi:
2 năm trước
Cho các tập hợp khác rỗng \(A=\left[ {m - 1;\dfrac{{m + 3}}{2}} \right]\) và \(B = \left( { - \infty ; - 3} \right) \cup \left[ {3; + \infty } \right)\). Tập hợp các giá trị thực của \(m\) để \(A \cap B \ne \emptyset \) là
Trả lời bởi giáo viên
Đáp án đúng: c
Để \(A \cap B \ne \emptyset \) thì điều kiện là \(\left\{ \begin{array}{l}m - 1 \le \dfrac{{m + 3}}{2}\\\left[ \begin{array}{l}m - 1 < - 3\\\dfrac{{m + 3}}{2} \ge 3\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 5\\\left[ \begin{array}{l}m < - 2\\m \ge 3\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m \le 5\\m < - 2\end{array} \right.\\\left\{ \begin{array}{l}m \le 5\\m \ge 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < - 2\\3 \le m \le 5\end{array} \right.\).
Vậy \(m \in \left( { - \infty - 2} \right) \cup \left[ {3;5} \right]\)
Minh họa bằng trục số
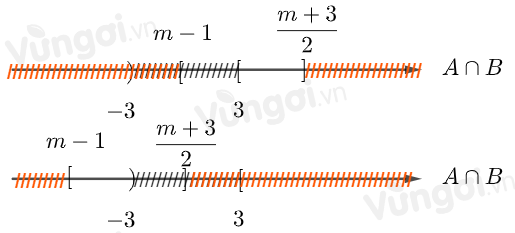
Hướng dẫn giải:
Hai tập hợp có giao khác rỗng nếu chúng có ít nhất \(1\) điểm chung.
