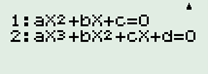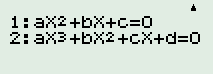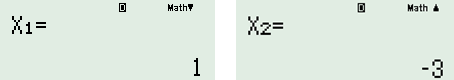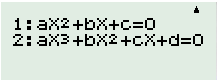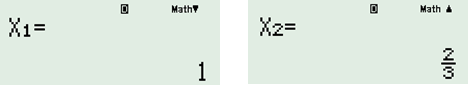Cho tập hợp: \(A = \left\{ {x \in \mathbb{Q}|\left( {2x - 1} \right)\left( {x - 3} \right)\left( {3{x^2} - 10x + 3} \right) = 0} \right\}\)
Tổng của phần tử lớn nhất và nhỏ nhất nằm trong tập hợp \(A\) là:
Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: \(3{x^2} - 10x + 3 = 0\)
\(\left( {2x - 1} \right)\left( {x - 3} \right)\left( {3{x^2} - 10x + 3} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}2x - 1 = 0\\x - 3 = 0\\3{x^2} - 10x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\x = 3\\x = 3\\x = \dfrac{1}{3}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\x = \dfrac{1}{3}\\x = 3\end{array} \right.\)
Mà \(x \in \mathbb{Q} \Rightarrow x \in \left\{ {\dfrac{1}{3};\,\,\dfrac{1}{2};\,\,3} \right\}\)\( \Rightarrow A = \left\{ {\dfrac{1}{3};\,\,\dfrac{1}{2};\,\,3} \right\}\)
Tổng của phần tử lớn nhất và phần tử nhỏ nhất của tập hợp \(A\) là: \(\dfrac{1}{3} + 3 = \dfrac{{10}}{3}\)
Viết tập hợp \(A = \left\{ {x \in \mathbb{N}|\left( {x + 2} \right)\left( {x - 3} \right)\left( {{x^2} - 5x + 6} \right) = 0} \right\}\) bằng cách liệt kê phần tử.
Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: \({x^2} - 5x + 6 = 0\)
\(\left( {x + 2} \right)\left( {x - 3} \right)\left( {{x^2} - 5x + 6} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 3 = 0\\{x^2} - 5x + 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 3\\x = 3\\x = 2\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\\x = 3\end{array} \right.\)
Vì \(x \in \mathbb{N}\) nên \(x = 2;\,\,x = 3\).
\( \Rightarrow A = \left\{ {2;\,\,3} \right\}.\)
Tổng tất cả các phần tử thuộc tập hợp \(A = \left\{ {x \in \mathbb{R}|2{x^3} - 11{x^2} + 17x - 6 = 0} \right\}\) là:
Nhấn “MODE” + “5” + “2” để giải phương trình bậc ba: \(2{x^3} - 11{x^2} + 17x - 6 = 0\)
\( \Rightarrow A = \left\{ {\dfrac{1}{2};\,\,2;\,\,3} \right\}\)
Tổng tất cả các phần tử thuộc tập hợp A là: \(\dfrac{1}{2} + 2 + 3 = \dfrac{{11}}{2}\)
Trong số thực sau, số thực nào không thuộc tập hợp \(A = \left\{ {x \in \mathbb{R}|\left( {2{x^2} - 3x + 1} \right)\left( {{x^2} - 3} \right) = 0} \right\}\)?
Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: \(2{x^2} - 3x + 1 = 0\)
Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: \({x^2} - 3 = 0\)
\(\left( {2{x^2} - 3x + 1} \right)\left( {{x^2} - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2{x^2} - 3x + 1 = 0\\{x^2} - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x_1} = 1\\{x_2} = \dfrac{1}{2}\\{x_3} = \sqrt 3 \\{x_4} = - \sqrt 3 \end{array} \right.\)
Vậy \(A = \left\{ { - \sqrt 3 ;\,\,\dfrac{1}{2};\,\,1;\,\,\sqrt 3 } \right\}\).
Khi đó \(\sqrt 2 \) không thuộc $A$.
Phần tử nhỏ nhất của tập hợp \(A = \left\{ {x \in \mathbb{Z}|\left( {{x^2} - 4} \right)\left( {2{x^2} - 5x + 2} \right) = 0} \right\}\) là:
\(\left( {{x^2} - 4} \right)\left( {2{x^2} - 5x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - 4 = 0\\2{x^2} - 5x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\\x = 2\\x = \dfrac{1}{2}\end{array} \right.\)
\( \Rightarrow A = \left\{ { - 2;\,\,2} \right\}.\)
Phần tử nhỏ nhất của tập A là $-2$
Số phần tử của tập hợp \(A = \left\{ {x \in \mathbb{R}|6{x^3} - 13{x^2} + x + 2 = 0} \right\}\) là:
Giải phương trình: \(6{x^3} - 13{x^2} + x + 2 = 0\)
+) Nhấn “MODE” + “5” + “Ñ” + “2” để giải phương trình bậc \(3\).
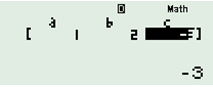
+) Nhập các hệ số \(a,\,\,b,\,\,c,\,\,d\) (Nhập xong 1 hệ số ta nhấn “\( = \)” để tiếp tục nhập hệ số tiếp theo)
+) Nhấn “=” ta được kết quả:
Mà \(x \in \mathbb{R}\) nên \(x \in \left\{ { - \dfrac{1}{3};\,\,\dfrac{1}{2};\,\,2} \right\}\).
Suy ra, \(A = \left\{ { - \dfrac{1}{3};\,\,\dfrac{1}{2};\,\,2} \right\}\).
Vậy tập hợp \(A\) có \(3\) phần tử.
Tập hợp \(A = \left\{ {x \in \mathbb{N}|{x^2} + 2x - 3 = 0} \right\}\) có tất cả bao nhiêu phần tử?
Giải phương trình: \({x^2} + 2x - 3 = 0\)
+) Nhấn “MODE” + “5” + “Ñ” + “1” để giải phương trình bậc \(2\).
+) Nhập các hệ số \(a,\,\,b,\,\,c\) (Nhập xong 1 hệ số ta nhấn “\( = \)” đẻ tiếp tục nhập hệ số tiếp theo)
+) Nhấn “\( = \)” ta được kết quả:
Vì \(x \in \mathbb{N}\) nên \(x = 1\).
Vậy tập hợp \(A\) có \(1\) phần tử.
Liệt kê các phần tử của tập hợp \(A = \left\{ {x \in \mathbb{Z}|3{x^2} - 5x + 2 = 0} \right\}\).
Giải phương trình: \(3{x^2} - 5x + 2 = 0\)
+) Nhấn “MODE” + “5” + “Ñ” + “1” để giải phương trình bậc \(2\).
+) Nhập các hệ số \(a,\,\,b,\,\,c\) (Nhập xong 1 hệ số ta nhấn “\( = \)” đẻ tiếp tục nhập hệ số tiếp theo)
+) Nhấn “\( = \)” ta được kết quả:
Vì \(x \in \mathbb{Z}\) nên \(x = 1\).
Vậy \(A = \left\{ 1 \right\}\).
Cho hai tập hợp khác rỗng \(A = \left[ {3m - 1;4} \right),B = \left( { - 3;{m^2} + 1} \right]\) với \(m \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) để tập \(A\) và tập \(B\) có phần tử chung duy nhất?
\(A\) và \(B\) có phần tử chung duy nhất
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}3m - 1 < 4\\ - 3 < {m^2} + 1\\3m - 1 = {m^2} + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3m < 5\\{m^2} > - 4\\{m^2} - 3m + 2 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < \dfrac{5}{3}\\\left[ \begin{array}{l}m = 2\\m = 1\end{array} \right.\end{array} \right. \Leftrightarrow m = 1.\end{array}\)
Cho hai tập hợp \(A=[0;5]\) và \(B=(2a; 3a+1],\) \(a>-1.\) Với giá trị nào của \(a\) thì \(A \cap B \ne \emptyset ?\)
\(A \cap B = \emptyset \Leftrightarrow \left\{ \matrix{ \left[ \matrix{ 2a \ge 5 \hfill \cr 3a + 1 < 0 \hfill \cr} \right. \hfill \cr a > - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ \left[ \matrix{ a \ge {5 \over 2} \hfill \cr a < - {1 \over 3} \hfill \cr} \right. \hfill \cr a > - 1 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ a \ge {5 \over 2} \hfill \cr - 1 < a < - {1 \over 3} \hfill \cr} \right.\)
\(\Rightarrow A \cap B \ne \emptyset \Leftrightarrow \left\{ \begin{array}{l}a < \frac{5}{2}\\\left[ \begin{array}{l}a \le - 1\\a \ge - \frac{1}{3}\end{array} \right.\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a < \frac{5}{2}\\a \le - 1\end{array} \right. \Leftrightarrow a \le - 1\\\left\{ \begin{array}{l}a < \frac{5}{2}\\a \ge - \frac{1}{3}\end{array} \right. \Leftrightarrow - \frac{1}{3} \le a < \frac{5}{2}\end{array} \right.\)
Mà \(a > - 1\) nên \( - \frac{1}{3} \le a < \frac{5}{2}\)
Hỏi tập hợp nào là tập hợp rỗng trong các tập hợp sau?
Ta có:
\( 6{x^2} - 7x + 1 = 0 \Leftrightarrow \left[ \matrix{ x = 1 \hfill \cr x = \dfrac{1}{6} \hfill \cr} \right.\)\( \Rightarrow x = 1\,\,\left( {x \in \mathbb{Z}} \right) \)\(\Rightarrow \) loại A.
\(\left| x \right| < 1 \Leftrightarrow - 1 < x < 1 \Rightarrow x = 0\,\,\left( {x \in \mathbb{Z}} \right)\)
\( \Rightarrow \) loại B.
\( {x^2} - 4x + 2 = 0 \Leftrightarrow \left[ \matrix{ x = 2 + \sqrt 2 \hfill \cr x = 2 - \sqrt 2 \hfill \cr} \right.\)\( \Rightarrow x \in \emptyset \,\,\left( {x \in \mathbb{Q}} \right)\)\( \Rightarrow \) Chọn C.
\( {x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \matrix{ x = 1 \hfill \cr x = 3 \hfill \cr} \right. \)\(\Rightarrow \) loại D.
Các câu sau đây,có bao nhiêu câu là mệnh đề?
(1) Ở đây đẹp quá!
(2) Phương trình \({x^2} - 3x + 1 = 0\) vô nghiệm
(3) $16$ không là số nguyên tố
(4) Hai phương trình \({x^2} - 4x + 3 = 0\) và \({x^2} - \sqrt {x + 3} + 1 = 0\) có nghiệm chung.
(5) Số \(\pi \) có lớn hơn \(3\) hay không?
(6) Italia vô địch Worldcup $2006$
(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.
(8) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.
Câu $(1)$ và $(5)$ không là mệnh đề (vì là câu cảm thán, câu hỏi)
Các câu $(3), (4), (6)$ là những mệnh đề đúng
Câu $(2),(7)$ và $(8)$ là những mệnh đề sai.
Vậy có \(6\) mệnh đề.
Trong một trận đấu có bốn đội tham gia là \(A,B,C,D\). Trước khi thi đấu, ba bạn Dung, Quang, Trung dự đoán như sau:
Dung: \(B\) nhì, còn \(C\) ba.
Quang: \(A\) nhì, còn \(C\) tư.
Trung: \(B\) nhất và \(D\) nhì.
Kết quả, mỗi bạn dự đoán đúng một đội và sai một đội. Hỏi mỗi đội đã đạt giải mấy?
Ta xét dự đoán của bạn Dung, giả sử dự đoán \(B\) nhì của Dung đúng thì dẫn đến\(B\) nhất của Trung là sai do đó \(D\) nhì của Trung là đúng (mâu thuẫn giả thiết \(B\) nhì)
Như vậy \(C\) thứ ba là đúng suy ra \(A\) nhì \(B\) nhất và \(D\) thứ tư.
Nêu mệnh đề phủ định của mệnh đề sau, cho biết mệnh đề này đúng hay sai?
\(K:\) " Phương trình \({x^4} - 2{x^2} + 2 = 0\) có nghiệm "
\(\overline K :\) " Phương trình \({x^4} - 2{x^2} + 2 = 0\) vô nghiệm ", mệnh đề này đúng vì \({x^4} - 2{x^2} + 2 = {\left( {{x^2} - 1} \right)^2} + 1 > 0\)
Phát biểu mệnh đề \(P \Leftrightarrow Q\) và xét tính đúng sai của nó với:
\(P:\) "Tứ giác \(ABCD\) là hình thoi" và \(Q:\)" Tứ giác \(ABCD\) là hình bình hành có hai đường chéo vuông góc với nhau"
Ta có mệnh đề \(P \Leftrightarrow Q\) đúng vì mệnh đề \(P \Rightarrow Q,\,\,Q \Rightarrow P\) đều đúng và được phát biểu như sau:
"Tứ giác \(ABCD\) là hình thoi khi và chỉ khi tứ giác \(ABCD\) là hình bình hành có hai đường chéo vuông góc với nhau" hoặc "Tứ giác \(ABCD\) là hình thoi nếu và chỉ nếu tứ giác \(ABCD\) là hình bình hành có hai đường chéo vuông góc với nhau"
Phát biểu mệnh đề \(P \Rightarrow Q\) và phát biểu mệnh đề đảo, xét tính đúng sai của các mệnh đề đó với: $P:\,\,\,''2 > 9''$ và $Q:\,\,''4 < 3''$. Chọn đáp án đúng:
Mệnh đề \(P \Rightarrow Q\) là " Nếu \(2 > 9\) thì \(4 < 3\)", mệnh đề này đúng vì mệnh đề \(2 > 9\) sai.
Mệnh đề đảo là \(Q \Rightarrow P\) : " Nếu \(4 < 3\) thì \(2 > 9\)", mệnh đề này đúng vì mệnh đề \(4 < 3\) sai.
Phát biểu mệnh đề phủ định của mệnh đề \(K:\) " Bất phương trình \({x^{2013}} > 2030\) vô nghiệm " và xét tính đúng sai của nó.
Mệnh đề phủ định của mệnh đề \(K\) là \(\overline K :\)" Bất phương trình \({x^{2013}} > 2030\) có nghiệm ", mệnh đề này đúng, cụ thể có thể chọn giá trị \(x = 2\) thỏa mãn bất phương trình.
Cho các mệnh đề :
A : “Nếu $\Delta ABC$ đều có cạnh bằng $a,$ đường cao là $h$ thì $h = \dfrac{{a\sqrt 3 }}{2}$”
B : “Tứ giác có bốn cạnh bằng nhau là hình vuông”
C : “$15$ là số nguyên tố”
D : “\(\sqrt {225} \) là một số nguyên”
Chọn câu sai:
Đáp án A: Mệnh đề $A \Rightarrow B$ sai vì $A$ đúng và $B$ sai \(\Rightarrow\) A đúng.
Đáp án B: Mệnh đề $A \Leftrightarrow D$ đúng vì hai mệnh đề $A$ và $D$ đều đúng \(\Rightarrow\) đáp án B đúng.
Đáp án C: Mệnh đề $B \Leftrightarrow C$ đúng vì hai mệnh đề $B$ và $C$ đều sai \(\Rightarrow\) đáp án C đúng.
Đáp án D: Mệnh đề $A \Rightarrow D$ đúng vì $A$ và $D$ đều đúng \(\Rightarrow\) đáp án D sai.
Cho hai mệnh đề: $P{\rm{ }}:$ " \(\sqrt 2 - \sqrt 3 > - 1\)" và $Q:$"\({\left( {\sqrt 2 - \sqrt 3 } \right)^2} > {\left( { - 1} \right)^2}\) "
Xét tính đúng sai của các mệnh đề \(P \Rightarrow Q,\overline Q \Rightarrow P\) ta được:
Ta có: Mệnh đề $P$ đúng, $Q$ sai.
Mệnh đề \(\overline Q :\) “\({\left( {\sqrt 2 - \sqrt 3 } \right)^2} \le {\left( { - 1} \right)^2}\)” là mệnh đề đúng.
\(P \Rightarrow Q\): " Nếu \(\sqrt 2 - \sqrt 3 > - 1\) thì \({\left( {\sqrt 2 - \sqrt 3 } \right)^2} > {\left( { - 1} \right)^2}\) "
\(\overline Q \Rightarrow P\): " Nếu \({\left( {\sqrt 2 - \sqrt 3 } \right)^2} \le {\left( { - 1} \right)^2}\) thì \(\sqrt 2 - \sqrt 3 > - 1\) "
Mệnh đề \(P \Rightarrow Q\) sai vì $P$ đúng, $Q$ sai, mệnh đề \(\overline Q \Rightarrow P\) đúng vì \(\overline Q \) và \(P\) đều đúng.
Cho mệnh đề chứa biến "\(P\left( x \right):x > {x^3}\)”. Chọn kết luận đúng:
Đáp án A:\(P\left( 1 \right):1 > {1^3}\) đây là mệnh đề sai nên A sai.
Đáp án B: $P\left( {\dfrac{1}{3}} \right):\dfrac{1}{3} > {\left( {\dfrac{1}{3}} \right)^3}$ đây là mệnh đề đúng nên B đúng.
Đáp án C: \(\forall x \in N,\,\,x > {x^3}\) là mệnh đề sai vì \(P\left( 1 \right)\) là mệnh đề sai nên C sai.
Đáp án D: \(\exists x \in N,\,\,x > {x^3}\) là mệnh đề sai vì \(x - {x^3} = x\left( {1 - x} \right)\left( {1 + x} \right) \le 0\) với mọi số tự nhiên nên không tồn tại số tự nhiên \(x\) nào thỏa mãn \(x > {x^3}\) nên D sai.