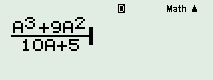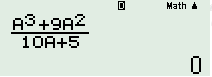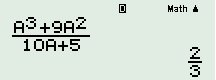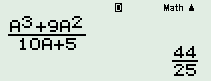Dùng các kí hiệu \(\forall ,\exists \) để viết lại mệnh đề sau và viết mệnh đề phủ định của nó: \(Q:\) “Với mọi số thực thì bình phương của nó là một số không âm”
Ta có \(Q:\,\forall x \in \mathbb{R},\,\,{x^2} \ge 0\), mệnh đề phủ định là \(\overline Q :\,\exists x \in \mathbb{R},\,\,{x^2} < 0\)
Xác định tính đúng sai của mệnh đề sau và tìm phủ định của mệnh đề: $B:$" Tồn tại số tự nhiên là số nguyên tố".
Mệnh đề $B$ đúng và \(\overline B \) : “Mọi số tự nhiêu đều không phải là số nguyên tố"
Cho mệnh đề chứa biến: \(P\left( x \right):\,''{x^2} - 2x \ge 0''\) với \(x \in \mathbb{R}\). Giá trị của \(x\) nào dưới đây làm cho \(P\left( x \right)\) đúng?
+ Với \(x = \dfrac{1}{4}\) ta có \({\left( {\dfrac{1}{4}} \right)^2} - 2.\dfrac{1}{4} = - \dfrac{7}{{16}} < 0\) nên \(P\left( {\dfrac{1}{4}} \right)\) sai.
+ Với $x = 2$ ta có \({2^2} - 2.2 = 0 \ge 0\) nên \(P\left( 2 \right)\) là mệnh đề đúng.
+ Với \(x = 1\) thì \({1^2} - 2.1 = - 1 < 0\) nên \(P\left( 1 \right)\) sai.
+ Với \(x = 0,5\) thì \({0,5^2} - 2.0,5 = - \dfrac{3}{4} < 0\) nên \(P\left( {0,5} \right)\) sai.
Tìm mệnh đề sai trong các mệnh đề dưới đây:
Đáp án A: Mệnh đề \(\forall x \in \mathbb{R},\,\,{x^3} - {x^2} + 1 > 0\) sai chẳng hạn khi $x = - 1$ ta có \({\left( { - 1} \right)^3} - {\left( { - 1} \right)^2} + 1 = - 1 < 0\)
Đáp án B: Mệnh đề \(\forall x \in \mathbb{R},\,\,{x^4} - {x^2} + 1 = \left( {{x^2} + \sqrt 3 x + 1} \right)\left( {{x^2} - \sqrt 3 x + 1} \right)\) đúng vì
\(\,{x^4} - {x^2} + 1 = {\left( {{x^2} + 1} \right)^2} - 3{x^2} = \left( {{x^2} + \sqrt 3 x + 1} \right)\left( {{x^2} - \sqrt 3 x + 1} \right)\)
Đáp án C: Mệnh đề \(\exists x \in N,\,\,{n^2} + 3\) chia hết cho $4$ đúng vì \(n = 1 \in N\)và \({n^2} + 3 = 4 \vdots 4\)
Đáp án D: Mệnh đề "\(\forall n \in N,\,n\left( {n + 1} \right)\) là một số chẵn" đúng vì \(n,n + 1\) là hai số tự nhiên liên tiếp và trong hai số tự nhiên liên tiếp luôn có \(1\) số chẵn nên tích của chúng chia hết cho \(2\) (là một số chẵn)
Cho mệnh đề $P:$ "Với mọi số thực $x,$ nếu $x$ là số hữu tỉ thì $2x$ là số hữu tỉ".
Xác định tính đúng - sai của các mệnh đề \(P,\overline P \)
Mệnh đề $P:$$''\forall x \in R,x \in \mathbb{Q} \Rightarrow 2x \in \mathbb{Q}''$. Mệnh đề này đúng vì \(x \in \mathbb{Q},2 \in \mathbb{Q}\) nên $2x \in \mathbb{Q}$
Vì mệnh đề $P$ đúng nên mệnh đề $\overline P$ sai.
Cho số tự nhiên $n.$ Xét hai mệnh đề chứa biến :$A\left( n \right): $"$n$ là số chẵn", $B\left( n \right): $"${n^2}$ là số chẵn". Hãy phát biểu mệnh đề “$\forall n \in \mathbb{N},\,\,B(n) \Rightarrow A(n)$”.
“$\forall n \in \mathbb{N},\,\,B(n) \Rightarrow A(n)$” : Với mọi số tự nhiên $n,$ nếu ${n^2}$ là số chẵn thì $n$ là số chẵn.
Cho tập hợp $A = \left\{ {1,2,3,4,a,b} \right\}$. Xét các mệnh đề sau đây:
$\left( I \right)$: “$3 \in A$”.
$\left( {II} \right)$: “$\left\{ {3,4} \right\} \in A$”.
$\left( {III} \right)$: “$\left\{ {a,3,b} \right\} \in A$”.
Trong các mệnh đề sau, mệnh đề nào đúng
$3$ là một phần tử của tập hợp $A$.
$\left\{ {3,4} \right\}$ là một tập con của tập hợp $A$. Ký hiệu: $\left\{ {3,4} \right\} \subset A$.
$\left\{ {a,3,b} \right\}$ là một tập con của tập hợp $A$. Ký hiệu: $\left\{ {a,3,b} \right\} \subset A$.
Trong các tập hợp sau, tập hợp nào là tập hợp rỗng:
$A = \left\{ {{\rm{x}} \in \mathbb{Z}\left| {\left| {\rm{x}} \right| < 1} \right.} \right\} \Rightarrow A = \left\{ 0 \right\}.$
$B = \left\{ {{\rm{x}} \in \mathbb{Z}\left| {6{x^2} - 7x + 1 = 0} \right.} \right\}$.
Ta có $6{x^2} - 7x + 1 = 0$ $ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{1}{6} \notin \mathbb{Z}\end{array} \right.$ $ \Rightarrow B = \left\{ 1 \right\}.$
$C = \left\{ {{\rm{x}} \in \mathbb{Q}\left| {{{\rm{x}}^{\rm{2}}} - 4x + 2 = 0} \right.} \right\}$.
Ta có ${x^2} - 4x + 2 = 0$ $ \Leftrightarrow \left[ \begin{array}{l}x = 2 - \sqrt 2 \notin \mathbb{Q}\\x = 2 + \sqrt 2 \notin \mathbb{Q}\end{array} \right.$ $ \Rightarrow C = \emptyset $
$D = \left\{ {{\rm{x}} \in \mathbb{R}\left| {{x^2} - 4x + 3 = 0} \right.} \right\}$.
Ta có ${x^2} - 4x + 3 = 0$ $ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.$ $ \Rightarrow D = \left\{ {1;\,3} \right\}.$
Cho tập hợp \(X = \left\{ {1;2;3;4} \right\}\). Câu nào sau đây đúng?
Số tập con của tập hợp \(X\) là: \({2^4} = 16\) nên A đúng.
Các tập hợp con có \(2\) phần tử của \(X\) là:
\(\left\{ {1;2} \right\},\left\{ {1;3} \right\},\left\{ {1;4} \right\},\left\{ {2;3} \right\},\left\{ {2;4} \right\},\left\{ {3;4} \right\}\)
Có \(6\) tập hợp con gồm \(2\) phần tử nên B sai.
Số tập con của tập hợp \(X\) chứa số \(1\) là: \(8\) nên C sai.
Đó là các tập hợp: \(\left\{ 1 \right\}\), \(\left\{ {1;2} \right\},\left\{ {1;3} \right\}\), \(\left\{ {1;4} \right\}\), \(\left\{ {1;2;3} \right\}\), \(\left\{ {1;2;4} \right\}\), \(\left\{ {1;3;4} \right\}\), \(\left\{ {1;2;3;4} \right\}.\)
Số tập con có $3$ phần tử của tập hợp \(X\) là: \(4\), cụ thể: \(\left\{ {1;2;3} \right\},\left\{ {1;2;4} \right\},\left\{ {2;3;4} \right\},\left\{ {1;3;4} \right\}\) nên D sai.
Cho \(A = \left[ { - 3;2} \right)\). Tập hợp\({C_\mathbb{R}}A\) là :
\({C_\mathbb{R}}A = \left( { - \infty ; + \infty } \right)\backslash \left[ { - 3;2} \right)\)\( = \left( { - \infty ;\, - 3} \right) \cup \left[ {2;\, + \infty } \right).\)
Trong các khẳng định sau khẳng định nào đúng:
A sai vì \(\mathbb{R}\backslash \mathbb{Q} = I\)
B sai vì ${\mathbb{N}^*} \subset \mathbb{N} \Rightarrow {\mathbb{N}^*} \cup \mathbb{N} = \mathbb{N}$
C sai vì ${\mathbb{N}^*} \subset \mathbb{Z} \Rightarrow {\mathbb{N}^*} \cap \mathbb{Z} = {\mathbb{N}^*}$
D đúng do ${\mathbb{N}^*} \subset \mathbb{Q} \Rightarrow {\mathbb{N}^*} \cap \mathbb{Q} = {\mathbb{N}^*}$
Cho các tập hợp:
\(M = \){$x \in \mathbb{N}\left| x \right.\,$ là bội số của \(2\)}.
\(N = \){$x \in \mathbb{N}\left| x \right.\,$ là bội số của \(6\)}.
\(P = \){$x \in \mathbb{N}\left| x \right.\,$là ước số của \(2\)}.
\(Q = \){$x \in \mathbb{N}\left| x \right.\,$là ước số của \(6\)}.
Mệnh đề nào sau đây đúng?
\( +M = \left\{ {0;\,2;\,4;\,6;\,8;\,10 ;\,12;...} \right\};\) $N = \left\{ {0;\,6;\,12;...} \right\}$$ \Rightarrow N \subset M,M \cap N = N.$
$ + \;P = \left\{ {1;\,2} \right\};$ $Q = \left\{ {1;\,2;\,3;\,6} \right\}$ $ \Rightarrow \,\,P \subset Q,\,\,P \cap Q = P$
Cho\(A = \left\{ {0;1;2;3;4} \right\},B = \left\{ {2;3;4;5;6} \right\}.\) Tập hợp \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right)\)bằng?
$A = \left\{ {0;1;2;3;4} \right\},B = \left\{ {2;3;4;5;6} \right\}.$
$A\backslash B = \left\{ {0;1} \right\},\,\,B\backslash A = \left\{ {5;6} \right\}$$ \Rightarrow \left( {A\backslash B} \right) \cup \left( {B\backslash A} \right) = \left\{ {0;1;5;6} \right\}$
Cho tập hợp \({C_\mathbb{R}}A = \left[ { - 3;\sqrt 8 } \right)\), \({C_\mathbb{R}}B = \left( { - 5;2} \right) \cup \left( {\sqrt 3 ;\sqrt {11} } \right).\) Tập \({C_\mathbb{R}}\left( {A \cap B} \right)\) là:
${C_\mathbb{R}}A = \left[ { - 3;\sqrt 8 } \right)$, ${C_\mathbb{R}}B = \left( { - 5;2} \right) \cup \left( {\sqrt 3 ;\sqrt {11} } \right) = \left( { - 5;\,\sqrt {11} } \right)$
$A = \left( { - \infty ;\, - 3} \right) \cup \left[ {\sqrt 8 ; + \infty } \right)$, $B = \left( { - \infty ; - 5} \right] \cup \left[ {\sqrt {11} ; + \infty } \right).$
$ \Rightarrow A \cap B = \left( { - \infty ; - 5} \right] \cup \left[ {\sqrt {11} ; + \infty } \right)$$ \Rightarrow {C_\mathbb{R}}\left( {A \cap B} \right) = \left( { - 5;\sqrt {11} } \right).$
Cho số thực \(a < 0\). Điều kiện cần và đủ để \(\left( { - \infty ;9a} \right) \cap \left( {\dfrac{4}{a}; + \infty } \right) \ne \emptyset \) là:
$\left( { - \infty ;9a} \right) \cap \left( {\dfrac{4}{a}; + \infty } \right) \ne \emptyset \,\,\left( {a < 0} \right) $ $\Leftrightarrow \,\,\dfrac{4}{a} < 9a\,$ $ \Leftrightarrow \,\,\dfrac{4}{a} - 9a\,\, < 0\,$
$ \Leftrightarrow \dfrac{{4 - 9{a^2}}}{a} < 0$$ \Leftrightarrow \left\{ \begin{array}{l}4 - 9{a^2} > 0\\a < 0\,\,\end{array} \right.$\( \Leftrightarrow \left\{ \begin{array}{l} - \dfrac{2}{3} < a < \dfrac{2}{3}\\a < 0\end{array} \right.\)
$ \Leftrightarrow - \dfrac{2}{3} < a < 0$.
Cho hai tập hợp \(A = \left\{ {x \in R:x + 2 \ge 0} \right\},\) \(B = \left\{ {x \in R:5 - x \ge 0} \right\}.\)
Khi đó \(A\backslash B\) là:
Bước 1:
Ta có \(A = \left\{ {x \in R:x + 2 \ge 0} \right\}\)\( \Rightarrow A = \left[ { - 2;\, + \infty } \right)\),
\(B = \left\{ {x \in R:5 - x \ge 0} \right\}\)\( \Rightarrow B = \left( { - \infty ;\,5} \right]\).
Bước 2:
Biểu diễn trên trục số:
Ta gạch bỏ phần không thuộc tập hợp A (Màu xanh) và phần thuộc tập hợp B (Màu cam) thì được hiệu (phần không bị gạch):

\( \Rightarrow A\backslash B = \left( {5;\, + \infty } \right).\)
Cho hai tập khác rỗng $A = \left( {m - 1;4} \right];B = \left( { - 2;2m + 2} \right),m \in \mathbb{R}$. Tìm $m$ để $A \cap B \ne \emptyset $.
+ Do $A,B \ne \emptyset $ ta có điều kiện $\left\{ \begin{array}{l}m - 1 < 4\\2m + 2 > - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 5\\m > - 2\end{array} \right. $ $\Leftrightarrow - 2 < m < 5$
Để $A \cap B = \emptyset \Leftrightarrow 2m + 2 \le m - 1 \Leftrightarrow m \le - 3$ (không thỏa điều kiện $ - 2 < m < 5$)
Do đó không có giá trị nào của \(m\) để \(A \cap B = \emptyset \)
Vậy với mọi \(m \in \left( { - 2;5} \right)\) thì \(A \cap B \ne \emptyset \)
Đáp án B sai vì học sinh không tìm điều kiện.
Đáp án C sai vì học sinh giải sai $m - 1 > - 2 \Leftrightarrow m > - 1$ và kết hợp với điều kiện.
Đáp án D sai vì học sinh giải sai $4 < 2m + 2 \Leftrightarrow m > 1$. Kết hợp với điều kiện
Cho $2$ tập khác rỗng $A = \left( {m - 1;4} \right];B = \left( { - 2;2m + 2} \right),m \in \mathbb{R}$. Tìm $m$ để $A \subset B$.
Với $2$ tập khác rỗng $A,B$ ta có điều kiện $\left\{ \begin{array}{l}m - 1 < 4\\2m + 2 > - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 5\\m > - 2\end{array} \right. $ $\Leftrightarrow - 2 < m < 5$
Để $A \subset B \Leftrightarrow \left\{ \begin{array}{l}m - 1 \ge - 2\\2m + 2 > 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge - 1\\2m + 2 > 4\end{array} \right. $ $\Leftrightarrow \left\{ \begin{array}{l}m \ge - 1\\m > 1\end{array} \right. \Leftrightarrow m > 1$
So với điều kiện $1 < m < 5$
Đáp án B sai vì học sinh không giải điều kiện.
Đáp án C sai vì học sinh giải:
Với $2$ tập khác rỗng $A, B$ ta có điều kiện $\left\{ \begin{array}{l}m - 1 < 4\\2m + 2 > - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 5\\m > - 2\end{array} \right. $ $\Leftrightarrow - 2 < m < 5$
Để $A \subset B \Leftrightarrow m - 1 \ge - 2 \Leftrightarrow m \ge - 1$. Kết hợp với điều kiện được kết quả $ - 1 \le m < 5$
Đáp án D sai vì học sinh giải $A \subset B \Leftrightarrow \left\{ \begin{array}{l}m - 1 < - 2\\2m + 2 < 4\end{array} \right. $ $\Leftrightarrow \left\{ \begin{array}{l}m < - 1\\m < 1\end{array} \right. \Leftrightarrow m < - 1$
Kết hợp với điều kiện $ - 2 < m < - 1$
Cho tập khác rỗng $A = \left[ {a;8 - a} \right],a \in \mathbb{R}$. Với giá trị nào của $a$ thì tập $A$ sẽ là một đoạn có độ dài $5$?
Điều kiện $a \le 8 - a \Leftrightarrow a \le 4$.
Khi đó để tập $A$ có độ dài là $5$ thì $8 - a - a = 5 \Leftrightarrow a = \dfrac{3}{2}$(thỏa điều kiện).
Đáp án B sai vì học sinh giải $a - \left( {8 - a} \right) = 5 \Leftrightarrow a = \dfrac{{13}}{2}$
Đáp án C sai vì học sinh giải $8 - a = 5 \Leftrightarrow a = 3$.
Đáp án D sai vì học sinh chỉ giải $a < 8 - a \Leftrightarrow a < 4$.
Liệt kê các phần tử tập hợp \(A = \left\{ {\left. {x = \dfrac{{{a^3} + 9{a^2}}}{{10a + 5}}} \right|a \in \mathbb{N},\,\,a \le 2} \right\}\).
*) Vì \(a \in \mathbb{N},\,\,a \le 2 \Rightarrow a \in \left\{ {0;\,\,1;\,\,2} \right\}\).
*) Nhập biểu thức của \(x\) vào máy tính.
*) Thay lần lượt giá trị của \(a\) vào biểu thức để tìm \(x\).
Với \(a = 0\): Nhấn phím “CALC” + “0” + “=” ta được:
Với \(a = 1\): Nhấn phím “CALC” + “1” + “=” ta được:
Với \(a = 2\): Nhấn phím “CALC” + “2” + “=” ta được:
\( \Rightarrow A = \left\{ {0;\,\,\dfrac{2}{3};\,\,\dfrac{{44}}{{25}}} \right\}\)