Trong các tập hợp sau đây, tập hợp nào không phải là tập rỗng?
*) \(A = \left\{ {x \in \mathbb{Q}|{x^2} - 4x + 2 = 0} \right\}\)
Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: \({x^2} - 4x + 2 = 0\)
\({x^2} - 4x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 2 \\x = 2 - \sqrt 2 \end{array} \right.\)
Mà \(x \in \mathbb{Q}\) nên \(A = \emptyset \).
*) \(B = \left\{ {x \in \mathbb{R}|{x^2} - x + 1 = 0} \right\}\)
Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: \({x^2} - x + 1 = 0\).
\( \Rightarrow B = \emptyset \)
*) \(C = \left\{ {x \in \mathbb{N}|{x^2} + 7x + 12 = 0} \right\}\)
Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: \({x^2} + 7x + 12 = 0\).
\({x^2} + 7x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 4\end{array} \right.\)
Mà \(x \in \mathbb{N} \Rightarrow C = \emptyset \).
*) \(D = \left\{ {x \in \mathbb{R}|{x^2} - 4x + 2 = 0} \right\}\)
Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: \({x^2} - 4x + 2 = 0\)
\({x^2} - 4x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 2 \\x = 2 - \sqrt 2 \end{array} \right.\)
Mà \(x \in \mathbb{R}\) nên \(D = \left\{ {2 - \sqrt 2 ;\,\,2 + \sqrt 2 } \right\}\).
Cho hai tập hợp: \(A = \left\{ {x \in \mathbb{Z}|\left( {{x^2} - 2} \right)\left( {{x^2} + 9} \right) = 0} \right\}\) và \(B = \left\{ {x \in \mathbb{N}|\left( {x + 1} \right)\left( {x - 2} \right)\left( {{x^2} - 7x + 6} \right) = 0} \right\}\)
Tổng số phần tử của tập hợp \(A\) và tập hợp \(B\) là:
*) \(A = \left\{ {\left. {x \in \mathbb{Z}} \right|\left( {{x^2} - 2} \right)\left( {{x^2} + 9} \right) = 0} \right\}\)
\(\left( {{x^2} - 2} \right)\left( {{x^2} + 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - 2 = 0\\{x^2} + 9 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 2 \\x = - \sqrt 2 \end{array} \right.\)
Mà \(x \in \mathbb{Z}\) nên \(A = \emptyset \).
*) Tập hợp B:
\(B=\left\{ {x \in \mathbb{N}|\left( {x + 1} \right)\left( {x - 2} \right)\left( {{x^2} - 7x + 6} \right) = 0} \right\}\)
Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: \({x^2} - 7x + 6 = 0\)
\(\left( {x + 1} \right)\left( {x - 2} \right)\left( {{x^2} - 7x + 6} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 2 = 0\\{x^2} - 7x + 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\\x = 6\\x = 1\end{array} \right.\)
Mà \(x \in \mathbb{N}\) nên \(B = \left\{ {1;\,\,2\,;\,\,6} \right\}\).
Số phần tử của tập hợp \(A\) và \(B\) là: \(0 + 3 = 3\) (phần tử).
Cho hai tập hợp \(A = \left[ { - 1;3} \right)\) và \(B = \left[ {a;\,a + 3} \right] \) . Với giá trị nào của a thì \( A \cap B = \emptyset ? \)
TH1:
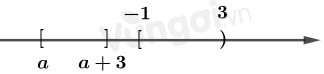
TH2:
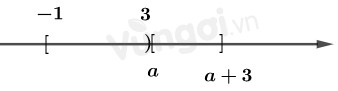
\(A \cap B = \emptyset \Leftrightarrow \left[ \matrix{ a + 3 < - 1 \hfill \cr a \ge 3 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ a < - 4 \hfill \cr a \ge 3 \hfill \cr} \right.\)
Cho hai tập hợp $A=\left\{0; 1; 2; 3; 4 \right\} $ và $B= \left\{2; 3; 4 ;5 ;6\right\}$. Tập hợp \( A\backslash B \) bằng:
Ta có: \( A\backslash B = \left\{ {0;\,1} \right\}. \)





