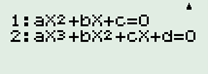Câu hỏi:
3 năm trước
Số phần tử của tập hợp \(A = \left\{ {x \in \mathbb{R}|6{x^3} - 13{x^2} + x + 2 = 0} \right\}\) là:
Trả lời bởi giáo viên
Đáp án đúng: d
Giải phương trình: \(6{x^3} - 13{x^2} + x + 2 = 0\)
+) Nhấn “MODE” + “5” + “Ñ” + “2” để giải phương trình bậc \(3\).
+) Nhập các hệ số \(a,\,\,b,\,\,c,\,\,d\) (Nhập xong 1 hệ số ta nhấn “\( = \)” để tiếp tục nhập hệ số tiếp theo)
+) Nhấn “=” ta được kết quả:
Mà \(x \in \mathbb{R}\) nên \(x \in \left\{ { - \dfrac{1}{3};\,\,\dfrac{1}{2};\,\,2} \right\}\).
Suy ra, \(A = \left\{ { - \dfrac{1}{3};\,\,\dfrac{1}{2};\,\,2} \right\}\).
Vậy tập hợp \(A\) có \(3\) phần tử.
Hướng dẫn giải:
Sử dụng chức năng giải phương trình bậc ba của máy tính bỏ túi.