Câu hỏi:
2 năm trước
Cho biết tập hợp tất cả các giá trị của tham số \(m\) để phương trình \(2\left( {{x^2} + \dfrac{1}{{{x^2}}}} \right) - 3\left( {x + \dfrac{1}{x}} \right) - 2m + 1 = 0\) có nghiệm là \(S = \left[ { - \dfrac{a}{b}; + \infty } \right)\), với \(a\), \(b\) là các số nguyên dương và \(\dfrac{a}{b}\) là phân số tối giản. Tính \(T = a + b\).
Trả lời bởi giáo viên
Đáp án đúng: d
Điều kiện xác định: $x \ne 0$. Đặt \(t = x + \dfrac{1}{x}\)\( \Rightarrow {t^2} - 2 = {x^2} + \dfrac{1}{{{x^2}}} \ge 2\)\( \Rightarrow \left| t \right| \ge 2\)\( \Leftrightarrow \left[ \begin{array}{l}t \ge 2\\t \le - 2\end{array} \right.\).
Phương trình đã cho trở thành \(2\left( {{t^2} - 2} \right) - 3t - 2m + 1 = 0\)\( \Leftrightarrow 2{t^2} - 3t - 2m - 3 = 0\)
\( \Leftrightarrow 2{t^2} - 3t - 3 = 2m\) (1)
Xét hàm số \(y = f\left( t \right) = 2{t^2} - 3t - 3\) có bảng biến thiên
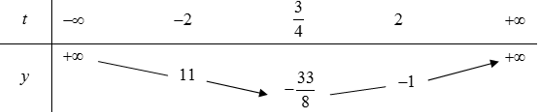
(1) có nghiệm $t$ thỏa \(\left[ \begin{array}{l}t \ge 2\\t \le - 2\end{array} \right.\) khi \(\left[ \begin{array}{l}2m \ge - 1\\2m \ge 11\end{array} \right.\)\( \Leftrightarrow m \ge - \dfrac{1}{2}\)\( \Rightarrow S = \left[ { - \dfrac{1}{2}; + \infty } \right)\).
Vậy \(T = 3\).
Hướng dẫn giải:
Đưa phương trình về ẩn \(t = x + \dfrac{1}{x}\) và tìm điều kiện để phương trình này có nghiệm ứng với yêu cầu bài toán (sử dụng phương pháp hàm số)
Câu hỏi khác
- Bài tập đại cương về phương trình toán 10 có lời giải
- Bài tập phương trình bậc nhất và bậc hai một ẩn toán 10 có lời giải
- Bài tập phương trình bậc ba, bậc bốn quy về bậc nhất, bậc hai toán 10 có lời giải
- Bài tập phương trình chứa dấu giá trị tuyệt đối toán 10 có lời giải
- Bài tập phương trình chứa căn toán 10 có lời giải
