Câu hỏi:
2 năm trước
Hỏi có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình x4−x2x2+5x+6≤0 ?
Trả lời bởi giáo viên
Đáp án đúng: d
Bất phương trình x4−x2x2+5x+6≤0 ⇔x2(x2−1)x2+5x+6≤0(∗)
Vì x2≥0,∀x∈R nên bất phương trình
(∗)⇔[x2=0x2−1x2+5x+6≤0 ⇔[x=0f(x)=x2−1x2+5x+6≤0
Phương trình x2−1=0⇔[x=1x=−1 và x2+5x+6=0⇔[x=−2x=−3.
Bảng xét dấu
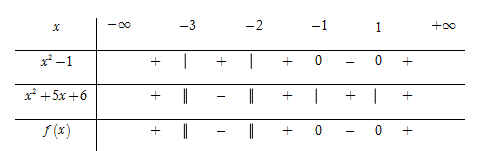
Dựa vào bảng xét dấu, ta thấy f(x)≤0⇔x∈(−3;−2)∪[−1;1]
Kết hợp với x∈Z, ta được x={−1;0;1}.
Vậy có tất cả 3 giá trị nguyên cần tìm.
Hướng dẫn giải:
- Biến đổi bất phương trình đưa về tích, thương các tam thức bậc hai và nhị thức bậc nhất.
- Xét dấu các tam thức bậc hai và nhị thức bậc nhất, từ đó suy ra nghiệm của bất phương trình

