Trả lời bởi giáo viên
Đáp án đúng: c
Điều kiện: x2−3x−10≠0⇔(x+2)(x−5)≠0⇔{x≠−2x≠5.
Bất phương trình −2x2+7x+7x2−3x−10≤−1⇔−2x2+7x+7x2−3x−10+1≤0 ⇔−x2+4x−3x2−3x−10≤0(∗)
Bảng xét dấu
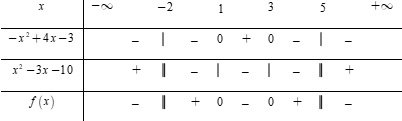
Dựa vào bảng xét dấu, bất phương trình (∗)⇔x∈(−∞;−2)∪[1;3]∪(5;+∞).
Hướng dẫn giải:
- Đặt điều kiện xác định.
- Chuyển vế, thu gọn bất phương trình, đưa về tích, thương các tam thức bậc hai và nhị thức bậc nhất.
- Xét dấu các tam thức bậc hai và nhị thức bậc nhất, từ đó suy ra nghiệm của bất phương trình.

