Phương trình $\left| {x - 2} \right|\left( {x + 1} \right) + m = 0$ có ba nghiệm phân biệt, giá trị thích hợp của tham số $m$ là:
Trả lời bởi giáo viên
Xét $\left| {x - 2} \right|\left( {x + 1} \right) + m = 0 \left( 1 \right)$
Với \(x \ge 2\), ta có: \(\left( 1 \right) \Leftrightarrow \left( {x - 2} \right)\left( {x + 1} \right) + m = 0\) \( \Leftrightarrow m = - {x^2} + x + 2\)
Với \(x < 2\), ta có: \(\left( 1 \right) \Leftrightarrow - \left( {x - 2} \right)\left( {x + 1} \right) + m = 0\) \( \Leftrightarrow m = {x^2} - x - 2\)
Đặt \(f\left( x \right) = \left\{ \begin{array}{l} - {x^2} + x + 2{\rm{ }} & {\rm{khi }}x \ge 2\\{x^2} - x - 2{\rm{ }} & {\rm{khi }}x < 2\end{array} \right.\)
Bảng biến thiên:
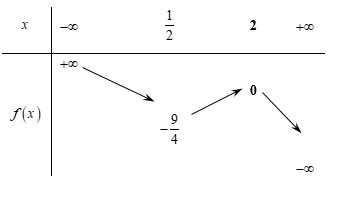
Dựa vào bảng biến thiên ta có \( - \dfrac{9}{4} < m < 0\).
Hướng dẫn giải:
- Phá dấu giá trị tuyệt đối đưa về các phương trình tương ứng.
- Cô lập \(m\), xét các hàm số trong khoảng tương ứng và tìm \(m\) để phương trình có \(3\) nghiệm phân biệt.

