Câu hỏi:
2 năm trước
Cho tam giác \(OAB\) vuông cân tại \(O,\) cạnh \(OA = a.\) Khẳng định nào sau đây sai ?
Trả lời bởi giáo viên
Đáp án đúng: c
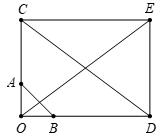
Dựa vào các đáp án, ta có nhận xét sau:
A đúng, gọi \(C\) nằm trên tia đối của tia \(AO\) sao cho \(OC = 3\,OA\)\( \Rightarrow 3\,\overrightarrow {OA} = \overrightarrow {OC} .\)
Và \(D\) nằm trên tia đối của tia \(BO\) sao cho \(OD = 4\,OB\)\( \Rightarrow 4\,\overrightarrow {OB} = \overrightarrow {OD} .\)
Dựng hình chữ nhật \(OCED\) suy ra \(\overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OE} \) (quy tắc hình bình hành).
Ta có \(\left| {3\overrightarrow {OA} + 4\overrightarrow {OB} } \right| = \left| {\overrightarrow {OC} + \overrightarrow {OD} } \right| = \left| {\overrightarrow {OE} } \right| = OE = CD = \sqrt {O{C^2} + O{D^2}} = 5a.\)
B đúng, vì \(\left| {2\,\overrightarrow {OA} } \right| + \left| {3\,\overrightarrow {OB} } \right| = 2\left| {\overrightarrow {OA} } \right| + 3\left| {\overrightarrow {OB} } \right| = 2a + 3a = 5a.\)
C sai, xử lý tương tự như ý đáp án A.
D đúng, vì \(\left| {11\,\overrightarrow {OA} } \right| - \left| {6\,\overrightarrow {OB} } \right| = 11\left| {\overrightarrow {OA} } \right| - 6\left| {\overrightarrow {OB} } \right| = 11a - 6a = 5a.\)
Hướng dẫn giải:
Nhận xét tính đúng sai của từng đáp án và kết luận.
