Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông cân tại \(C\) và \(AB = \sqrt 2 .\) Tính độ dài của \(\overrightarrow {AB} + \overrightarrow {AC} .\)
Trả lời bởi giáo viên
Đáp án đúng: a
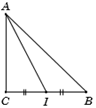
Ta có \(AB = \sqrt 2 \Rightarrow AC = CB = 1.\)
Gọi \(I\) là trung điểm \(BC\) \( \Rightarrow AI = \sqrt {A{C^2} + C{I^2}} = \dfrac{{\sqrt 5 }}{2}\)
Khi đó: \(\overrightarrow {AC} + \overrightarrow {AB} = 2\overrightarrow {AI} \)\( \Rightarrow \left| {\overrightarrow {AC} + \overrightarrow {AB} } \right| = 2\left| {\overrightarrow {AI} } \right| = 2.\dfrac{{\sqrt 5 }}{2} = \sqrt 5 \)
Hướng dẫn giải:
Tìm véc tơ tổng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \), từ đó suy ra độ dài.

