Câu hỏi:
2 năm trước
Gọi \(G\) là trọng tâm tam giác vuông \(ABC\) với cạnh huyền \(BC = 24\). Tính độ dài của vectơ \(\overrightarrow v = \overrightarrow {GB} + \overrightarrow {GC} \).
Trả lời bởi giáo viên
Đáp án đúng: c
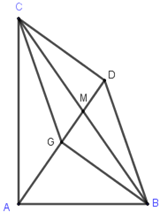
Dựng hình bình hành \(GBDC\). Gọi \(M\) là trung điểm \(BC\).
Khi đó ta có \(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right| = \left| {\overrightarrow {GD} } \right| = GD = 2GM\)\( = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{1}{2}BC = \dfrac{1}{3}BC = \dfrac{1}{3}.24 = 8\)
Hướng dẫn giải:
- Dựng hình bình hành \(GBDC\), sử dụng quy tắc hình bình hành tìm véc tơ tổng \(\overrightarrow {GB} + \overrightarrow {GC} \).
- Tính độ dài véc tơ tìm được ở trên và suy ra kết luận.

