Câu hỏi:
2 năm trước
Cho tam giác đều ABC cạnh a có G là trọng tâm. Độ dài của vec tơ \(\overrightarrow {AC} - \overrightarrow {BG} \) là
Trả lời bởi giáo viên
Đáp án đúng: d
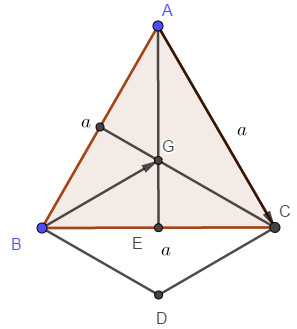
Ta có G là trọng tâm tam giác ABC nên \(GB \bot AC\) và \(GB = \dfrac{{a\sqrt 3 }}{3}\).
Vẽ hình bình hành \(BGCD\). Khi đó \(\overrightarrow {BG} = \overrightarrow {DC} \)\( \Rightarrow CD = \dfrac{{a\sqrt 3 }}{3}\)
\(\overrightarrow {AC} - \overrightarrow {BG} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)\( \Rightarrow \left| {\overrightarrow {AC} - \overrightarrow {BG} } \right| = AD\)
Vì \(GB \bot AC\) nên \(AC \bot CD\). Suy ra \(AD = \sqrt {{a^2} + \dfrac{{{a^2}}}{3}} = \dfrac{{2a\sqrt 3 }}{3}\).
Vậy \(\left| {\overrightarrow {AC} - \overrightarrow {BG} } \right| = \dfrac{{2a\sqrt 3 }}{3}\).
