Câu hỏi:
3 năm trước
Cho tam giác đều \(ABC\) cạnh \(a,\) \(H\) là trung điểm của \(BC\). Tính \(\left| {\overrightarrow {CA} - \overrightarrow {HC} } \right|.\)
Trả lời bởi giáo viên
Đáp án đúng: d
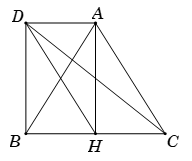
Gọi \(D\) là điểm thỏa mãn tứ giác \(ACHD\) là hình bình hành \(\Rightarrow CH = AD \Rightarrow AD = HB\).
\( \Rightarrow AHBD\) là hình chữ nhật \( \Rightarrow BD = AH\).
\(\left| {\overrightarrow {CA} - \overrightarrow {HC} } \right| = \left| {\overrightarrow {CA} + \overrightarrow {CH} } \right| = \left| {\overrightarrow {CD} } \right| = CD.\)
Ta có \(CD = \sqrt {B{D^2} + B{C^2}} = \sqrt {A{H^2} + B{C^2}} \)\( = \sqrt {\dfrac{{3{a^2}}}{4} + {a^2}} = \dfrac{{a\sqrt 7 }}{2}\)
Hướng dẫn giải:
Tìm hiệu hai véc tơ đã cho, từ đó tính độ dài và kết luận.

