Câu hỏi:
2 năm trước
Gọi \(O\) là tâm của hình vuông \(ABCD\). Vectơ nào trong các vectơ dưới đây bằng \(\overrightarrow {CA} ?\)
Trả lời bởi giáo viên
Đáp án đúng: c
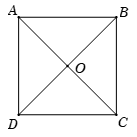
Xét các đáp án:
Đáp án A. Ta có \(\overrightarrow {BC} + \overrightarrow {AB} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} = - \overrightarrow {CA} .\)
Đáp án B. Ta có \( - \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OC} - \overrightarrow {OA} = \overrightarrow {AC} = - \overrightarrow {CA} .\)
Đáp án C. Ta có \(\overrightarrow {BA} + \overrightarrow {DA} = - \left( {\overrightarrow {AD} + \overrightarrow {AB} } \right) = - \overrightarrow {AC} = \overrightarrow {CA} .\)
Đáp án D. Ta có \(\overrightarrow {DC} - \overrightarrow {CB} = \overrightarrow {DC} + \overrightarrow {BC} = - \left( {\overrightarrow {CD} + \overrightarrow {CB} } \right) = - \overrightarrow {CA} .\)
Hướng dẫn giải:
Nhận xét tính đúng sai của mỗi đáp án, sử dụng quy tắc ba điểm đối với phép cộng và trừ hai véc tơ.
