Cho hình thang $ABCD$ có đáy $AB = a$, $CD = 2a$. Gọi $M$, $N$ lần lượt là trung điểm $AD$ và $BC$. Tính độ dài của véctơ $\overrightarrow {MN} + \overrightarrow {BD} + \overrightarrow {CA} $.
Trả lời bởi giáo viên
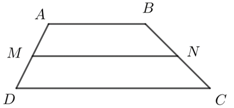
Ta có $M,\,N$ là trung điểm của $AD$ và $BC$ nên $\overrightarrow {MD} + \overrightarrow {MA} = \overrightarrow 0 $ và $\overrightarrow {BN} + \overrightarrow {CN} = \overrightarrow 0 $.
Khi đó: $\left| {\overrightarrow {MN} + \overrightarrow {BD} + \overrightarrow {CA} } \right| = \left| {\overrightarrow {MN} + \overrightarrow {BN} + \overrightarrow {NM} + \overrightarrow {MD} + \overrightarrow {CN} + \overrightarrow {NM} + \overrightarrow {MA} } \right|$
$ = \left| {\overrightarrow {MN} + 2\overrightarrow {NM} } \right| = \left| {\overrightarrow {NM} } \right| = NM = \dfrac{1}{2}\left( {AB + CD} \right) = \dfrac{{3a}}{2}$.
Hướng dẫn giải:
- Xen điểm tính véc tơ tổng của $\overrightarrow {MN} + \overrightarrow {BD} + \overrightarrow {CA} $
- Sử dụng kiến thức hình học đã biết tính độ dài véc tơ ở trên.

