Câu hỏi:
2 năm trước
Tìm a, c biết parabol (P): \(y = a{x^2} - 4x + c\) đi qua điểm \(A\left( {1;2} \right)\) và \(B\left( { - 2;5} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: a
Do A, B thuộc đồ thị (P), thay tọa độ của A, B vào phương trình của (P), ta được:
\(\left\{ \begin{array}{l}a.{\left( 1 \right)^2} - 4.1 + c = 2\\a.{\left( { - 2} \right)^2} - 4.\left( { - 2} \right) + c = 5\end{array} \right.\)
\(\begin{array}{l}\Leftrightarrow\left\{ \begin{array}{l}a - 4 + c = 2\\4a + 8 + c = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a+c = 6\\4a+c = -3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = - 3\\c = 9\end{array} \right.\end{array}\)
Vậy \(a = - 3;c = 9\).
Sử dụng MTCT casio fx 580 vnx giải hệ phương trình \(\left\{ \begin{array}{l}a+c = 6\\4a+c = -3\end{array} \right.\)
Bước 1: Chuyển sang chế độ giải hệ phương trình bậc nhất hai ẩn
Màn hình xuất hiện:
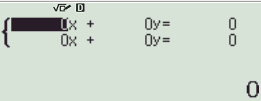
Bước 2: Nhập các hệ số vào tìm a và c
Hướng dẫn giải:
Thay tọa độ điểm \(A,B\) vào phương trình parabol, lập hệ hai phương trình hai ẩn tìm \(a, c\) và kết luận.
