Câu hỏi:
2 năm trước
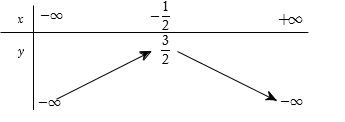
Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?
Trả lời bởi giáo viên
Đáp án đúng: d
Nhận xét:
Bảng biến thiên có bề lõm hướng xuống. Loại đáp án A và B.
Đỉnh của parabol có tọa độ là \(\left( { - \dfrac{1}{2};\dfrac{3}{2}} \right)\). Xét các đáp án còn lại, đáp án D thỏa mãn.
Hướng dẫn giải:
- Parabol \(y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) có tọa độ đỉnh là \(\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right).\)
- Nếu a > 0 thì hàm số tăng (đồng biến) trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\) và giảm (nghịch biến) trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\).
- Nếu a < 0 thì hàm số tăng (đồng biến) trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\) và giảm (nghịch biến) trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\).
