Câu hỏi:
2 năm trước
Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \({x^2} - 5x + 7 + 2m = 0\) có nghiệm thuộc đoạn \(\left[ {1;5} \right]\).
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có \({x^2} - 5x + 7 + 2m = 0 \Leftrightarrow {x^2} - 5x + 7 = - 2m.\) \(\left( * \right)\)
Phương trình \(\left( * \right)\) là phương trình hoành độ giao điểm của parabol \(\left( P \right):{x^2} - 5x + 7\) và đường thẳng \(y = - 2m\) (song song hoặc trùng với trục hoành).
Ta có bảng biến thiên của hàm số \(y = {x^2} - 5x + 7\) trên \(\left[ {1;5} \right]\) như sau:
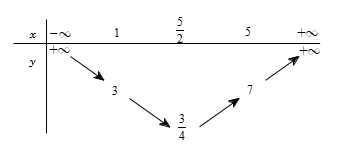
Dựa vào bảng biến ta thấy \(x \in \left[ {1;5} \right]\) thì \(y \in \left[ {\dfrac{3}{4};7} \right]\).
Do đó để phương trình \(\left( * \right)\) có nghiệm \(x \in \left[ {1;5} \right] \Leftrightarrow \dfrac{3}{4} \le - 2m \le 7 \Leftrightarrow - \dfrac{3}{8} \ge m \ge - \dfrac{7}{2}.\)
Hướng dẫn giải:
- Biến đổi phương trình về dạng \(f\left( x \right) = g\left( m \right)\).
- Lập bảng biến thiên của hàm số \(y = f\left( x \right)\) và sử dụng lý thuyết về mối tương giao đồ thị với số nghiệm của phương trình.
