Câu hỏi:
2 năm trước
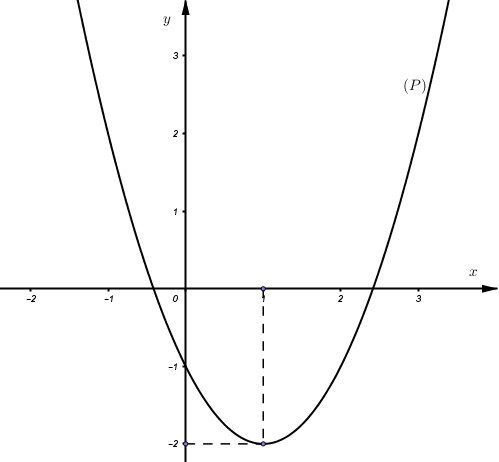
Cho đồ thị hàm số \(y = {x^2} - 2x - 1\left( P \right).\)Dựa vào đồ thị \(\left( P \right)\) xác định số giá trị nguyên dương của \(m\) để phương trình \({x^2} - 2x + 2m - 2 = 0\) có nghiệm \(x \in \left[ { - 1;2} \right]?\)
Trả lời bởi giáo viên
Đáp án đúng: c
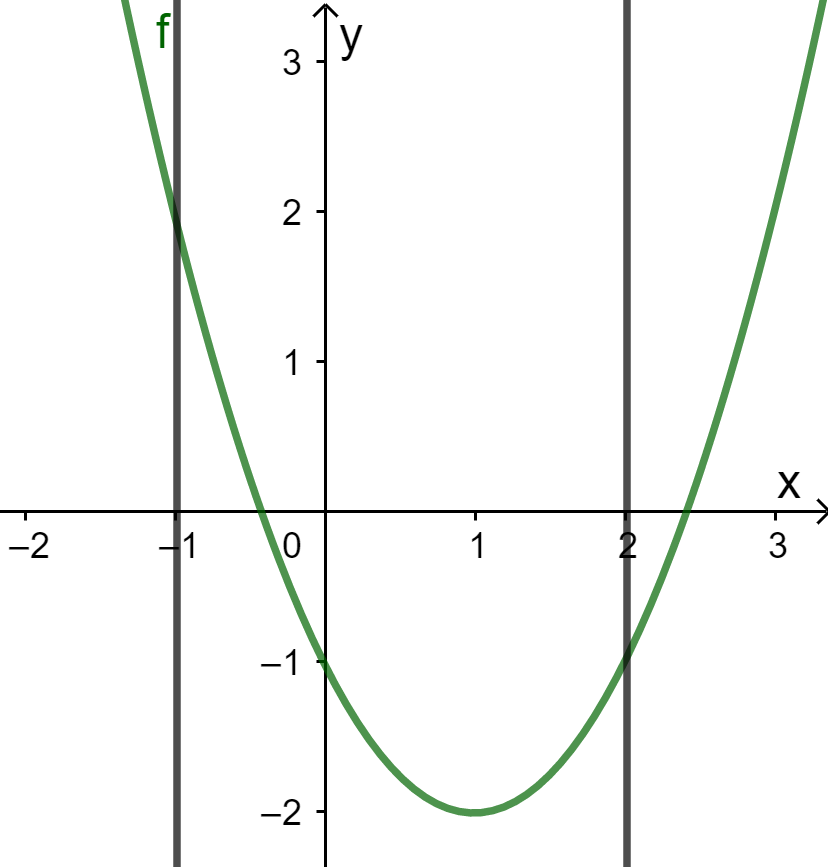
\({x^2} - 2x + 2m - 2 = 0\)\( \Leftrightarrow {x^2} - 2x - 1 = 1 - 2m\)
Đây là phương trình hoành độ giao điểm của đồ thị hàm số \(\left( P \right)\) và đường thẳng \(y = 1 - 2m\) song song \(Ox\)
Xét trong đoạn \(x \in \left[ { - 1;2} \right] \Rightarrow \)\(y \in \left[ { - 2;2} \right]\)
Suy ra để phương trình có nghiệm thì \( - 2 \le 1 - 2m \le 2\)\( \Leftrightarrow \dfrac{{ - 1}}{2} \le m \le \dfrac{3}{2}\) mà \(m \in {\mathbb{Z}^ + } \Rightarrow m = 1\)
Vậy để phương trình \({x^2} - 2x + 2m - 2 = 0\) có nghiệm thì \(m = 1\).
Hướng dẫn giải:
Đưa phương trình về phương trình hoành độ giao điểm của đồ thị hàm số \(y = {x^2} - 2x - 1\,\,\left( P \right)\) và đường thẳng song song trục Ox và biện luận trong khoảng \(x \in \left[ { - 1;2} \right]\)
