Câu hỏi:
2 năm trước
Đề chính thức ĐGNL HCM 2019
Một gia đình trồng rau và hoa trên diện tích 10 héc ta. Nếu trồng rau thì trên mỗi héc ta cần 10 công lao động và thu lợi 3 triệu đồng, nếu trồng hoa thì trên mỗi héc ta cần 20 công lao động và thu lợi 4 triệu đồng. Biết rằng số lao động không quá 160 . Gọi x, y lần lượt là số héc ta rau và hoa được trồng tương ứng để thu lợi nhuận cao nhất. Khi đó giá trị của $ x$ là:
Trả lời bởi giáo viên
Đáp án đúng: c
Điều kiện: $x\ge 0, y \ge 0$
Số công nhân là: $10x+20y$
Diện tích trồng rau và hoa là 10 hec ta nên ta có: $x+y \le 10$
Vì số công nhân không quá 160 người nên ta có: $10x+20y \le 160$
Khi đó $x,y$ phải thỏa mãn hệ: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 10\\10x + 20y \le 160\end{array} \right.\)
Biểu diễn tập nghiệm ta được miền nghiệm là tứ giác OABC với $O(0;0),A(10;0),B(4;6),C(0;8)$:
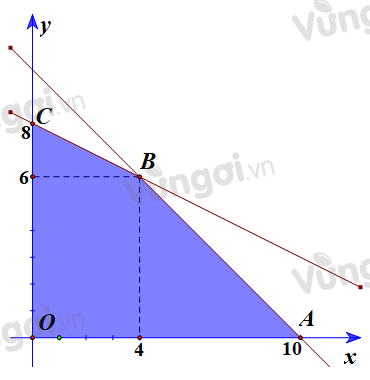
Lợi nhuận là $L=3x+4y$
$L(10;0)=30;L(4;6)=3.4+4.6=36;L(0;8)=4.8=32$
Xét giá trị của L tại các đỉnh O, A, B, C và so sánh ta suy ra $x=4;y=6$ là diện tích cần trồng để thu được nhiều lợi nhuận nhất $L=36$ triệu đồng.
Vậy $x=4$
Hướng dẫn giải:
- Đặt ẩn x,y và đặt điều kiện
- Biểu diễn các ẩn số thông qua dữ liệu đề bài cho
- Giải hệ bất phương trình vừa lập được
- Kết luận
Câu hỏi khác
- Bài tập bất phương trình và hệ bất phương trình bậc nhất hai ẩn toán 10 có lời giải
- Bài tập bất phương trình và hệ bất phương trình bậc nhất một ẩn toán 10 có lời giải
- Bài tập bất đẳng thức toán 10 có lời giải
- Bài tập dấu của nhị thức bậc nhất toán 10 có lời giải
- Bài tập đại cương về bất phương trình toán 10 có lời giải
