Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}\dfrac{x}{2} + \dfrac{y}{3} - 1 \ge 0\\x \ge 0\\x + \dfrac{1}{2} - \dfrac{{3y}}{2} \le 2\end{array} \right.\) chứa điểm nào trong các điểm sau đây?
Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.
Với \(O\left( {0;0} \right) \Rightarrow \)\(\left\{ \begin{array}{l}\dfrac{0}{2} + \dfrac{0}{3} - 1 \ge 0\\0 \ge 0\\0 + \dfrac{1}{2} - \dfrac{{3.0}}{2} \le 2\end{array} \right.\). Bất phương trình thứ nhất sai nên A sai.
Với \(M\left( {2;1} \right) \Rightarrow \)\(\left\{ \begin{array}{l}\dfrac{2}{2} + \dfrac{1}{3} - 1 \ge 0\\2 \ge 0\\2 + \dfrac{1}{2} - \dfrac{{3.1}}{2} \le 2\end{array} \right.\): Đúng.
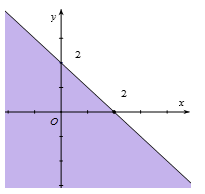
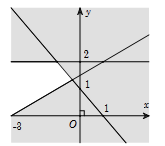
Miền nghiệm của bất phương trình \(x + y \le 2\) là phần tô đậm trong hình vẽ của hình vẽ nào, trong các hình vẽ sau?
Đường thẳng \(\Delta :x + y - 2 = 0\) đi qua hai điểm \(A\left( {2;0} \right),B\left( {0;2} \right)\).
Cặp số \(\left( {0;0} \right)\) thỏa mãn bất phương trình \(x + y \le 2\) vì (0-0 < 2 \).
Do đó miền nghiệm chứa điểm (0;0).
Kiểm tra các đáp án:
+) Hình 1 có vẽ đường thẳng \( x+y=2\) và miền tô đậm chứa điểm (0;0) nên biểu diễn miền nghiệm của bất phương trình \(x + y \le 2\) (thỏa mãn).
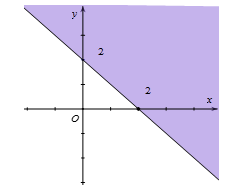
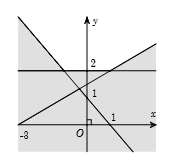
+) Hình 2 phần tô đậm không chứa (0;0) nên loại.
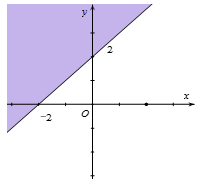
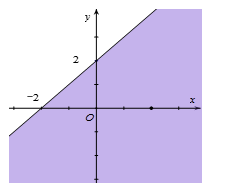
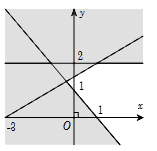
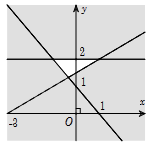
+) Hình 3 và 4 đều loại vì đường thẳng được vẽ lại là \(y=x-2\) hay \(x-y=2\) chứ không phải \(x+y=2\)
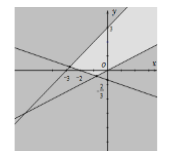
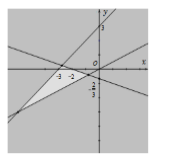
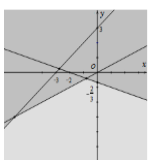
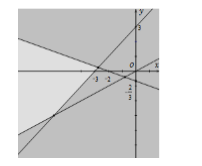
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\\y - x < 3\end{array} \right.\) là phần không tô đậm của hình vẽ nào trong các hình vẽ sau?
Chọn điểm \(M\left( {0;1} \right)\) thử vào các bất phương trình của hệ thấy thỏa mãn.
Quan sát các đáp án thì chỉ có đáp án A có miền không tô màu đậm chứa \(M\).
Phần tô đậm trong hình vẽ dưới đây (có chứa biên), biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
Phần tô đậm trong hình vẽ dưới đây (có chứa biên), biểu diễn tập nghiệm của bất phương trình \(1 \le x \le 2\)
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + y - 1 > 0\\y \ge 2\\ - x + 2y > 3\end{array} \right.\) là phần không tô đậm của hình vẽ nào trong các hình vẽ sau?
Chọn điểm \(M\left( {0;4} \right)\) thử vào các bất phương trình của hệ thấy thỏa mãn.
Đối chiếu các ĐA ta thấy, chỉ có đáp án B có miền không tô màu chứa điểm \(M\).
Phần tô đậm trong hình vẽ sau, biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
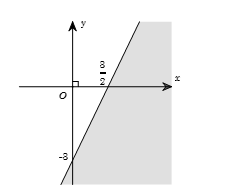
Đường thẳng đi qua hai điểm \(A\left( {\dfrac{3}{2};0} \right)\) và \(B\left( {0; - 3} \right)\) nên có phương trình \(2x - y = 3\).
Mặt khác, cặp số \(\left( {0;0} \right)\) không thỏa mãn bất phương trình \(2x - y > 3\) nên phần tô đậm ở hình trên biểu diễn miền nghiệm của bất phương trình \(2x - y > 3\).
Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
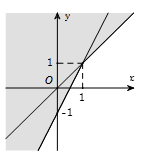
Do miền nghiệm không chứa biên nên ta loại đáp án A.
Chọn điểm \(M\left( {1;0} \right)\) thử vào các hệ bất phương trình.
Xét đáp án B, ta có \(\left\{ \begin{array}{l}1 - 0 > 0\\2.1 - 0 > 1\end{array} \right.\): Đúng và miền nghiệm không chứa biên.
Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
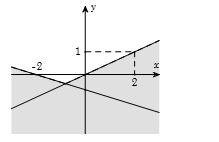
Do miền nghiệm không chứa biên nên ta loại đáp án A và C.
Chọn điểm \(M\left( {0;1} \right)\) thử vào các hệ bất phương trình.
Xét đáp án B, ta có \(\left\{ \begin{array}{l}0 - 2.1 > 0\\0 + 3.1 < - 2\end{array} \right.\): Sai.
Biểu thức $F\left( {x;y} \right) = y-x$ đạt giá trị nhỏ nhất với điều kiện $\left\{ {\begin{array}{*{20}{c}}{2x - y \ge 2}\\{x - 2y \le 2}\\{x + y \le 5}\\{x \ge 0}\end{array}} \right.$ tại điểm $M$ có toạ độ là:
Ta giải các hệ phương trình
$\left\{ \begin{array}{l}2x - y = 2\\x - 2y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{3}\\y = - \dfrac{2}{3}\end{array} \right.;$$\left\{ \begin{array}{l}2x - y = 2\\x + y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{7}{3}\\y = \dfrac{8}{3}\end{array} \right.;$ $\left\{ \begin{array}{l}x - 2y = 2\\x + y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 1\end{array} \right.$
Khi đó \(F\left( {x;y} \right)\) đạt GTNN tại một trong các điểm \(\left( {\dfrac{2}{3}; - \dfrac{2}{3}} \right),\left( {\dfrac{7}{3};\dfrac{8}{3}} \right),\left( {4;1} \right)\).
Đối chiếu các đáp án thì loại B và D.
Xét điểm \(\left( {\dfrac{2}{3}; - \dfrac{2}{3}} \right)\), thay tọa độ điểm này vào hệ ta thấy thỏa mãn nên nó thuộc miền nghiệm.
Xét điểm \(\left( {4;1} \right)\), thay tọa độ của điểm này vào hệ ta thấy thỏa mãn nên nó thuộc miền nghiệm.
Tính \(F\left( {\dfrac{2}{3}; - \dfrac{2}{3}} \right) = - \dfrac{2}{3} - \dfrac{2}{3} = - \dfrac{4}{3}\), \(F\left( {4;1} \right) = 1 - 4 = - 3 < - \dfrac{4}{3}\).
So sánh $F\left( {x;y} \right) = y-x$ đạt GTNN tại \(x = 4;y = 1\).
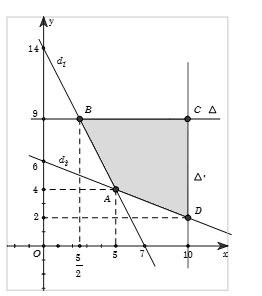
Giá trị nhỏ nhất \({F_{\min }}\) của biểu thức $F\left( {x;y} \right) = 4x + 3y$ trên miền xác định bởi hệ $\,\left\{ \begin{array}{l}0 \le \,\,x\,\, \le \,\,10\\0\,\, \le \,\,y\,\, \le \,\,9\\2x\,\, + \,\,y\,\, \ge \,\,14\\2x\,\, + \,\,5y\,\, \ge \,\,30\end{array} \right.$ là
Trong mặt phẳng tọa độ \(Oxy,\)vẽ các đường thẳng
\({d_1}:2x + y - 14 = 0,\,\,{\rm{ }}{d_2}:2x + 5y - 30 = 0,{\rm{ }}\Delta :y = 9,{\rm{ }}\Delta ':x = 10.\)
Khi đó miền nghiệm của hệ bất phương trình là phần mặt phẳng (tứ giác \(ABCD\) kể cả biên) tô màu như hình vẽ.
Xét các đỉnh của miền khép kín tạo bởi hệ là
\(A\left( {5;4} \right),B\left( {\dfrac{5}{2};9} \right),C\left( {10;9} \right),D\left( {10;2} \right).\)
Ta có $\left\{ \begin{array}{l}F\left( {5;4} \right) = 32\\F\left( {\dfrac{5}{2};9} \right) = 37\\F\left( {10;9} \right) = 67\\F\left( {10;2} \right) = 46\end{array} \right. \Rightarrow {F_{\min }} = 32.$
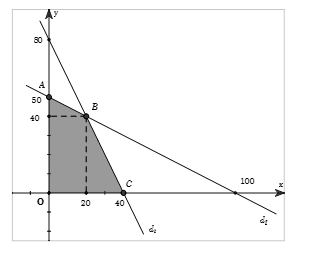
Cho $x,y$ thoả mãn hệ $\left\{ \begin{array}{l}x + 2y - 100 \le 0\\2x\,\, + \,y - 80\,\, \le 0\\x \ge 0\\y \ge 0\end{array} \right..$ Tìm giá trị lớn nhất \({P_{\max }}\) của biểu thức $P = \left( {x;y} \right) = 40000x + 30000y.$
Trong mặt phẳng tọa độ \(Oxy,\)vẽ các đường thẳng
\({d_1}:x + 2y - 100 = 0,\,\,{\rm{ }}{d_2}:2x + y - 80 = 0.\)
Khi đó miền nghiệm của hệ bất phương trình là phần mặt phẳng (tứ giác \(OABC\) kể cả biên) tô màu như hình vẽ.
Xét các đỉnh của miền khép kín tạo bởi hệ là
$\begin{array}{l}O\left( {0;0} \right),\,\,\\A\,\left( {0;50} \right),\,\,\\B\left( {20;40} \right),\\C\left( {40;0} \right).\end{array}$
Ta có \(\left\{ \begin{array}{l}P\left( {0;0} \right) = 0\\P\left( {0;50} \right) = 1500000\\P\left( {20;40} \right) = 2000000\\P\left( {40;0} \right) = 1600000\end{array} \right.\)
\( \Rightarrow {P_{\max }} = 2000000.\)
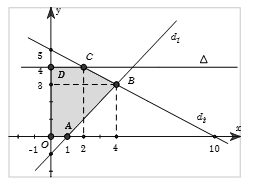
Giá trị lớn nhất \({F_{\max }}\) của biểu thức $F\left( {x;y} \right) = x + 2y$ trên miền xác định bởi hệ \(\left\{ \begin{array}{l}0 \le y \le 4\\x \ge 0\\x - y - 1 \le 0\\x + 2y - 10 \le 0\end{array} \right.\) là
Trong mặt phẳng tọa độ \(Oxy,\) vẽ các đường thẳng \({d_1}:x - y - 1 = 0,\)\({d_2}:x + 2y - 10 = 0,\) \(\Delta :y = 4\)
Khi đó miền nghiệm của hệ bất phương trình là phần mặt phẳng (ngũ giác \(OABCD\) kể cả biên) tô màu như hình vẽ.
Xét các đỉnh của miền khép kín tạo bởi hệ là
\(O\left( {0;0} \right),{\rm{ }}A\left( {1;0} \right),{\rm{ }}B\left( {4;3} \right),{\rm{ }}C\left( {2;4} \right),{\rm{ }}D\left( {0;4} \right).\)
Ta có $\left\{ \begin{array}{l}F\left( {0;0} \right) = 0\\F\left( {1;0} \right) = 1\\F\left( {4;3} \right) = 10\\F\left( {2;4} \right) = 10\\F\left( {0;4} \right) = 8\end{array} \right. \Rightarrow {F_{\max }} = 10.$
Một xưởng sản xuất hai loại sản phẩm
- Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 nghìn;
- Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30 nghìn.
Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất?
Gọi $x \ge 0,{\rm{ }}y \ge 0\,{\rm{ }}\left( {{\rm{kg}}} \right)$ lần lượt là số sản phẩm loại I và loại II cần sản xuất.
Khi đó, tổng số nguyên liệu sử dụng: \(2x + 4y \le 200.\)
Tổng số giờ làm việc: \(30x + 15y \le 1200.\)
Lợi nhuận tạo thành: \(L = 40x + 30y\) (nghìn).
Ta tìm \(x,y\) thỏa mãn hệ \(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\2x + 4y \le 200\\30x + 15y \le 1200\end{array} \right.\) sao cho \(L = 40x + 30y\) đạt giá trị lớn nhất.
Giải từng hệ phương trình:
\(\left\{ \begin{array}{l}x = 0\\y = 0\end{array} \right. \Rightarrow O\left( {0;0} \right)\)
\(\left\{ \begin{array}{l}x = 0\\2x + 4y = 200\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 50\end{array} \right.\)\( \Rightarrow B\left( {0;50} \right)\)
\(\left\{ \begin{array}{l}x = 0\\30x + 15y = 1200\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 80\end{array} \right.\)\( \Rightarrow C\left( {0;80} \right)\)
\(\left\{ \begin{array}{l}y = 0\\2x + 4y = 200\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 100\\y = 0\end{array} \right.\)\( \Rightarrow D\left( {100;0} \right)\)
\(\left\{ \begin{array}{l}y = 0\\30x + 15y = 1200\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 40\end{array} \right.\)\( \Rightarrow E\left( {0;40} \right)\)
\(\left\{ \begin{array}{l}2x + 4y = 200\\30x + 15y = 1200\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 20\\y = 40\end{array} \right.\) \( \Rightarrow F\left( {20;40} \right)\).
Thay tọa độ các điểm \(O,B,C,D,E,F\) vào biểu thức \(O,B,E,F\) thỏa mãn.
Tính giá trị \(L\) tại các điểm \(O,B,E,F\) ta thấy tại \(F\left( {20;40} \right)\) thì \(L\) đạt GTLN và \(L = 2000\).
Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm \(A\) và sản phẩm \(B\) trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm \(A\) lãi \(4\) triệu đồng người ta sử dụng máy \(I\) trong \(1\) giờ, máy \(II\) trong \(2\) giờ và máy \(III\) trong \(3\) giờ. Để sản xuất ra một tấn sản phẩm \(B\) lãi được \(3\) triệu đồng người ta sử dụng máy \(I\) trong \(6\) giờ, máy \(II\) trong \(3\) giờ và máy \(III\) trong \(2\) giờ. Biết rằng máy \(I\) chỉ hoạt động không quá \(36\) giờ, máy hai hoạt động không quá \(23\) giờ và máy \(III\) hoạt động không quá \(27\) giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất.
Gọi \(x \ge 0,{\rm{ }}y \ge 0\) (tấn) là sản lượng cần sản xuất của sản phẩm \(A\) và sản phẩm \(B.\) Ta có:
\(x + 6y\) là thời gian hoạt động của máy \(I.\)
\(2x + 3y\) là thời gian hoạt động của máy \(II.\)
\(3x + 2y\) là thời gian hoạt động của máy \(III.\)
Số tiền lãi của nhà máy: \(T = 4x + 3y\) (triệu đồng).
Bài toán trở thành: Tìm \(x \ge 0,{\rm{ }}y \ge 0\) thỏa mãn \(\left\{ \begin{array}{l}x + 6y \le 36\\2x + 3y \le 23\\3x + 2y \le 27\end{array} \right.\) để \(T = 4x + 3y\) đạt giá trị lớn nhất.
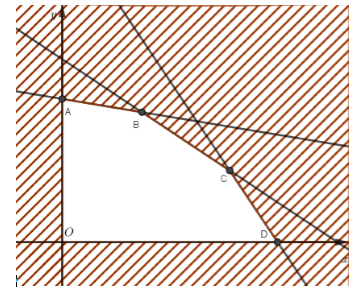
Miền nghiệm của hệ là ngũ giác \(OABCD\), ở đó \(O\left( {0;0} \right)\), \(A\left( {0;6} \right)\), \(B\left( {\dfrac{{10}}{3};\dfrac{{49}}{9}} \right)\), \(C\left( {7;3} \right)\), \(D\left( {9;0} \right)\).
Thay tọa độ các điểm vào biểu thức \(T\) ta được \({T_{\max }} = 36\) tại \(x = 7,y = 3\).
Bất phương trình nào sau đây là bất phương tình bậc nhất hai ẩn?
+ Bất phương trình \(2x^2+3y>6\) có bậc của x là 2 nên đây không là bất phương trình bậc nhất hai ẩn.
+ Ta có \({2^2}x + y \le 0 \Leftrightarrow 4x + y \le 0\)
=> a=4,b=1 và c=0. Các ẩn là x và y
=> \({2^2}x + y \le 0\) là bất phương trình bậc nhất hai ẩn.
+ \(2{x^2} - y \ge 1\) có bậc của x là 2 nên đây không là bất phương trình bậc nhất hai ẩn.
+ \(2x - y^2 \ge 1\) có bậc của y là 2 nên đây không là bất phương trình bậc nhất hai ẩn.
Nếu số tiền bán vé thu được nhỏ hơn 20 triệu đồng thì x và y thỏa mãn điều kiện gì?
Ta có 20 triệu = 20 000 000=\({2.10^7}\) (đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50000x + 100000y\) (đồng)
Số tiền thu được nhỏ hơn 20 triệu thì:
\(\begin{array}{l}50000x + 100000y < {2.10^7}\\ \Leftrightarrow x + 2y < 400\end{array}\)
Các số nguyên không âm x và y phải thoả mãn điều kiện gì để số tiền bán vé thu được đạt tối thiểu 20 triệu đồng?
Ta có 20 triệu = 20 000 000=\({2.10^7}\) (đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50000x + 100000y\) (đồng)
Nên để số tiền thu được tối thiểu 20 triệu thì ta cần:
\(\begin{array}{l}50000x + 100000y \ge {2.10^7}\\ \Leftrightarrow x + 2y \ge 400\end{array}\)
Viết biểu thức tính số tiền bán vé thu được (đơn vị nghìn đồng) ở rạp chiếu phim đó theo x và y.
Bước 1:
Số tiền bán x vé loại 1 là: \(x.50000\) (đồng)
Số tiền bán y vé loại 2 là: \(y.100000\) (đồng)
Bước 2:
Số tiền thu được là
\(50000x + 100000y\) (đồng)
Nhân dịp Tết Trung thu, một doanh nghiệp dự định sản xuất hai loại bánh: bánh nướng và bánh dẻo. Lượng đường cần cho mỗi chiếc bánh nướng, bánh dẻo lần lượt là 60 g, 50 g. Doanh nghiệp đã nhập về 500 kg đường.
Ta gọi x, y lần lượt là số bánh nướng và số bánh dẻo doanh nghiệp dự định sản xuất (x, y là số tự nhiên). Viết điều kiện ràng buộc đối với x và y để lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về.
Đổi 60g=0,06kg, 50g=0,05kg
Lượng đường cần cho x chiếc bánh nướng là 0,06x kg
Lượng đường cần cho y chiếc bánh dẻo là 0,05y kg
Vì lượng đường đã nhập về là 500kg và lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về nên ta có:
\(0,06x + 0,05y \le 500\)
Bất phương trình nào sau đây không là bất phương trình bậc nhất hai ẩn trong các bất phương trình sau:
A. \(5x + 3y < 20\)
Đây là bất phương trình bậc nhất hai ẩn.
B. \(3x - \dfrac{5}{y} > 2\)
Đây là không là bất phương trình bậc nhất hai ẩn vì có ẩn y ở mẫu.
C. \(7x + \dfrac{y}{2} < 2\)
Đây là bất phương trình bậc nhất hai ẩn.
D. \( \dfrac{x}{2}-3y < 2\)
Đây là bất phương trình bậc nhất hai ẩn.
