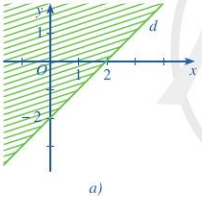
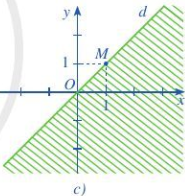
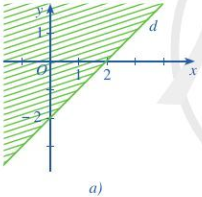
Biểu thức $F\left( {x;y} \right) = y-x$ đạt giá trị nhỏ nhất với điều kiện $\left\{ {\begin{array}{*{20}{c}}{2x - y \ge 2}\\{x - 2y \le 2}\\{x + y \le 5}\\{x \ge 0}\end{array}} \right.$ tại điểm $M$ có toạ độ là:

Ta giải các hệ phương trình

$\left\{ \begin{array}{l}2x - y = 2\\x - 2y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{3}\\y =  - \dfrac{2}{3}\end{array} \right.;$$\left\{ \begin{array}{l}2x - y = 2\\x + y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{7}{3}\\y = \dfrac{8}{3}\end{array} \right.;$ $\left\{ \begin{array}{l}x - 2y = 2\\x + y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 1\end{array} \right.$

Khi đó \(F\left( {x;y} \right)\) đạt GTNN tại một trong các điểm \(\left( {\dfrac{2}{3}; - \dfrac{2}{3}} \right),\left( {\dfrac{7}{3};\dfrac{8}{3}} \right),\left( {4;1} \right)\).

Đối chiếu các đáp án thì loại B và D.

Xét điểm \(\left( {\dfrac{2}{3}; - \dfrac{2}{3}} \right)\), thay tọa độ điểm này vào hệ ta thấy thỏa mãn nên nó thuộc miền nghiệm.

Xét điểm \(\left( {4;1} \right)\), thay tọa độ của điểm này vào hệ ta thấy thỏa mãn nên nó thuộc miền nghiệm.

Tính \(F\left( {\dfrac{2}{3}; - \dfrac{2}{3}} \right) =  - \dfrac{2}{3} - \dfrac{2}{3} =  - \dfrac{4}{3}\), \(F\left( {4;1} \right) = 1 - 4 =  - 3 <  - \dfrac{4}{3}\).

So sánh $F\left( {x;y} \right) = y-x$ đạt GTNN tại \(x = 4;y = 1\).