Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm \(A\) và sản phẩm \(B\) trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm \(A\) lãi \(4\) triệu đồng người ta sử dụng máy \(I\) trong \(1\) giờ, máy \(II\) trong \(2\) giờ và máy \(III\) trong \(3\) giờ. Để sản xuất ra một tấn sản phẩm \(B\) lãi được \(3\) triệu đồng người ta sử dụng máy \(I\) trong \(6\) giờ, máy \(II\) trong \(3\) giờ và máy \(III\) trong \(2\) giờ. Biết rằng máy \(I\) chỉ hoạt động không quá \(36\) giờ, máy hai hoạt động không quá \(23\) giờ và máy \(III\) hoạt động không quá \(27\) giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất.

Gọi \(x \ge 0,{\rm{ }}y \ge 0\) (tấn) là sản lượng cần sản xuất của sản phẩm \(A\) và sản phẩm \(B.\) Ta có:

    \(x + 6y\) là thời gian hoạt động của máy \(I.\)

    \(2x + 3y\) là thời gian hoạt động của máy \(II.\)

    \(3x + 2y\) là thời gian hoạt động của máy \(III.\)

Số tiền lãi của nhà máy: \(T = 4x + 3y\) (triệu đồng).

Bài toán trở thành: Tìm \(x \ge 0,{\rm{ }}y \ge 0\) thỏa mãn \(\left\{ \begin{array}{l}x + 6y \le 36\\2x + 3y \le 23\\3x + 2y \le 27\end{array} \right.\) để \(T = 4x + 3y\) đạt giá trị lớn nhất.

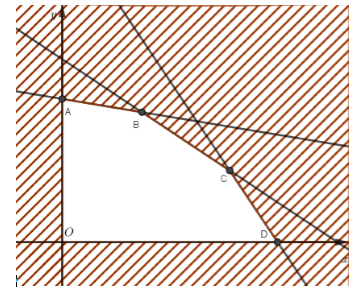
Miền nghiệm của hệ là ngũ giác \(OABCD\), ở đó \(O\left( {0;0} \right)\), \(A\left( {0;6} \right)\), \(B\left( {\dfrac{{10}}{3};\dfrac{{49}}{9}} \right)\), \(C\left( {7;3} \right)\), \(D\left( {9;0} \right)\).

Thay tọa độ các điểm vào biểu thức \(T\) ta được \({T_{\max }} = 36\) tại \(x = 7,y = 3\).