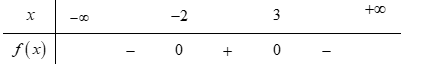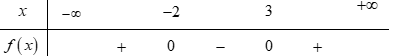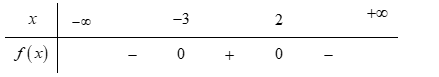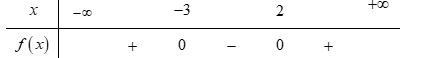Dấu của tam thức bậc hai

Ta có $f\left( x \right) = 0\, \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 2\end{array} \right.$.

Bảng xét dấu

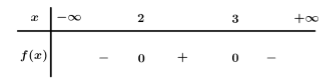
Dựa vào bảng xét dấu ta được

        $f\left( x \right) > 0$với $2 < x{\rm{ }} < 3$ và $f\left( x \right) < 0$ với $x < 2$ hoặc $x > 3$.

Ta có $f\left( x \right) = 0\, \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.$.

Bảng xét dấu

Dựa vào bảng xét dấu \(f\left( x \right) \le 0\, \Leftrightarrow \,1 \le x \le 3\).

Ta có $f\left( x \right) = 0\, \Leftrightarrow \left[ \begin{array}{l}x =  - 3\\x = \sqrt 2 \end{array} \right.$.

Bảng xét dấu

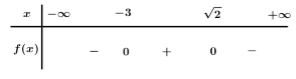
Dựa vào bảng xét dấu \(f\left( x \right) > 0\, \Leftrightarrow \, - 3 < x < \sqrt 2 \).

\({x^2} - 2x - m \le 0 \Leftrightarrow {x^2} - 2x \le m\)

Xét \(f\left( t \right) = {x^2} - 2x\) trên đoạn \(\left[ {0;3} \right]\), ta có bảng biến thiên

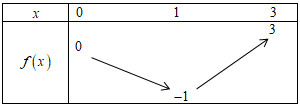
Vậy để bất phương trình \(f\left( t \right) = {x^2} - 2x \le m\) nghiệm đúng với mọi \(x \in \left[ {0;3} \right]\)

\( \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ {0;\,\,3} \right]} f\left( x \right) \Leftrightarrow m \ge 3\)

Ta có \( - {x^2} - x + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 3\\x = 2\end{array} \right.\)

Hệ số \(a =  - 1 < 0\)

Áp dụng định lý về dấu của tam thức bậc hai ta có đáp án C là đáp án cần tìm.

Phương trình vô nghiệm khi và chỉ khi \(\Delta  < 0 \Leftrightarrow {\left( {m + 1} \right)^2} - 4 < 0\)

\( \Leftrightarrow {m^2} + 2m - 3 < 0 \Leftrightarrow \left( {m - 1} \right)\left( {m + 3} \right) < 0 \Leftrightarrow  - \,3 < m < 1\).

Yêu cầu bài toán $ \Leftrightarrow $$\left\{ \begin{array}{l}a = 2{m^2} + 1 \ne 0\\\Delta ' = 4{m^2} - 2\left( {2{m^2} + 1} \right) =  - 2 < 0\end{array} \right.,\forall m \in \mathbb{R}.$

Vậy phương trình đã cho luôn vô nghiệm với mọi $m \in \mathbb{R}.$

Xét phương trình $\left( {m - 2} \right){x^2} + 2\left( {2m - 3} \right)x + 5m - 6 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left(  *  \right).$

TH1. Với $m - 2 = 0 \Leftrightarrow m = 2,$ khi đó $\left(  *  \right) \Leftrightarrow 2x + 4 = 0 \Leftrightarrow x =  - \,2.$

Suy ra với $m = 2$ thì phương trình $\left(  *  \right)$ có nghiệm duy nhất $x =  - \,2.$

Do đó $m = 2$ không thỏa mãn yêu cầu bài toán.

TH2. Với $m - 2 \ne 0 \Leftrightarrow m \ne 2,$ khi đó để phương trình $\left(  *  \right)$ vô nghiệm $ \Leftrightarrow \Delta ' < 0$

$ \Leftrightarrow {\left( {2m - 3} \right)^2} - \left( {m - 2} \right)\left( {5m - 6} \right) < 0$ $ \Leftrightarrow 4{m^2} - 12m + 9 - \left( {5{m^2} - 16m + 12} \right) < 0$

$ \Leftrightarrow  - \,{m^2} + 4m - 3 < 0$$ \Leftrightarrow {m^2} - 4m + 3 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 3\\m < 1\end{array} \right.$.

Do đó, với $\left[ \begin{array}{l}m > 3\\m < 1\end{array} \right.$ thì phương trình $\left(  *  \right)$ vô nghiệm.

Kết hợp hai TH, ta được $\left[ \begin{array}{l}m > 3\\m < 1\end{array} \right.$ là giá trị cần tìm.

Xét phương trình $m{x^2} - 2mx + 4 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left(  *  \right).$

TH1. Với $m = 0,$ khi đó phương trình $\left(  *  \right) \Leftrightarrow 4 = 0$ (vô lý).

Suy ra với $m = 0$ thì phương trình $\left(  *  \right)$ vô nghiệm.

TH2. Với $m \ne 0,$ khi đó để phương trình $\left(  *  \right)$ vô nghiệm $ \Leftrightarrow $$\Delta ' < 0$

$ \Leftrightarrow {m^2} - 4m < 0 \Leftrightarrow m\left( {m - 4} \right) < 0 \Leftrightarrow 0 < m < 4$

Kết hợp hai TH, ta được $0 \le m < 4$ là giá trị cần tìm.

Xét phương trình $\left( {{m^2} - 4} \right){x^2} + 2\left( {m - 2} \right)x + 3 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left(  *  \right).$

TH1. Với ${m^2} - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 2\\m =  - \,2\end{array} \right..$

$ \bullet $ Khi $m = 2 \Rightarrow \left(  *  \right) \Leftrightarrow 3 = 0$ (vô lý).

$ \bullet $ Khi $m =  - \,2 \Rightarrow \left(  *  \right) \Leftrightarrow  - \,8x + 3 = 0 \Leftrightarrow x = \dfrac{3}{8}.$

Suy ra với $m = 2$ thỏa mãn yêu cầu của bài toán.

TH2. Với ${m^2} - 4 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne 2\\m \ne  - \,2\end{array} \right.,$ khi đó để phương trình $\left(  *  \right)$ vô nghiệm $ \Leftrightarrow $$\Delta ' < 0$

$ \Leftrightarrow {\left( {m - 2} \right)^2} - 3\left( {{m^2} - 4} \right) < 0$ $ \Leftrightarrow {m^2} - 4m + 4 - 3{m^2} + 12 < 0$ $ \Leftrightarrow  - 2{m^2} - 4m + 16 < 0$

$ \Leftrightarrow {m^2} + 2m - 8 > 0$$ \Leftrightarrow \left( {m - 2} \right)\left( {m + 4} \right) > 0$ $ \Leftrightarrow \left[ \begin{array}{l}m > 2\\m <  - \,4\end{array} \right.$.

Suy ra với $\left[ \begin{array}{l}m > 2\\m <  - \,4\end{array} \right.$ thỏa mãn yêu cầu của bài toán.

Kết hợp hai TH, ta được $\left[ \begin{array}{l}m \ge 2\\m <  - 4\end{array} \right.$ là giá trị cần tìm.

Để phương trình $f\left( x \right) = 0$ có nghiệm $ \Leftrightarrow \Delta ' \ge 0 \Leftrightarrow {\left( { - b} \right)^2} - 4.3 \ge 0$

$ \Leftrightarrow {b^2} - 12 \ge 0 \Leftrightarrow {b^2} - {\left( {2\sqrt 3 } \right)^2} \ge 0$ $ \Leftrightarrow \left( {b - 2\sqrt 3 } \right)\left( {b + 2\sqrt 3 } \right) \ge 0$ $ \Leftrightarrow \left[ \begin{array}{l}b \ge 2\sqrt 3 \\b \le  - 2\sqrt 3 \end{array} \right.$

Vây $b \in \left( { - \infty ; - 2\sqrt 3 } \right] \cup \left[ {2\sqrt 3 ; + \infty } \right)$ là giá trị cần tìm.

Xét phương trình ${x^2} + 2\left( {m + 2} \right)x - 2m - 1 = 0,$ có $\Delta ' = {\left( {m + 2} \right)^2} + 2m + 1.$

Yêu cầu bài toán $ \Leftrightarrow \Delta ' > 0$ $ \Leftrightarrow {m^2} + 4m + 4 + 2m + 1 > 0$ $ \Leftrightarrow {m^2} + 6m + 5 > 0$

$ \Leftrightarrow \left( {m + 1} \right)\left( {m + 5} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}m >  - 1\\m <  - 5\end{array} \right.$ là giá trị cần tìm.

Xét $2{x^2} + 2\left( {m + 2} \right)x + 3 + 4m + {m^2} = 0,$ có $\Delta ' = {\left( {m + 2} \right)^2} - 2\left( {{m^2} + 4m + 3} \right).$

Yêu cầu bài toán $ \Leftrightarrow \Delta ' > 0$$ \Leftrightarrow {m^2} + 4m + 4 - 2{m^2} - 8m - 6 > 0$ $ \Leftrightarrow  - {m^2} - 4m - 2 > 0$

$ \Leftrightarrow {m^2} + 4m + 2 < 0$ $ \Leftrightarrow {\left( {m + 2} \right)^2} < 2$ $ \Leftrightarrow  - 2 - \sqrt 2  < m <  - 2 + \sqrt 2 $

Kết hợp với $m \in \mathbb{Z},$ ta được $m = \left\{ { - \,3; - \,2; - \,1} \right\}$ là các giá trị cần tìm.

Hàm số đã cho xác định khi và chỉ khi $5 - 4x - {x^2} \ge 0.$

Phương trình $5 - 4x - {x^2} = 0$ $ \Leftrightarrow {x^2} + 4x - 5 = 0$ $ \Leftrightarrow \left( {x - 1} \right)\left( {x + 5} \right) = 0$ $ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 5\end{array} \right.$

Bảng xét dấu

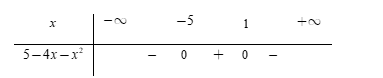
Dựa vào bảng xét dấu, ta thấy $5 - 4x - {x^2} \ge 0 \Leftrightarrow x \in \left[ { - \,5;1} \right].$

Vậy nghiệm dương lớn nhất để hàm số xác định là $x = 1.$

Hàm số xác định khi và chỉ khi \(4 - 3x - {x^2} > 0.\)

Phương trình \(4 - 3x - {x^2} = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x + 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - \,4\end{array} \right..\) Bảng xét dấu:

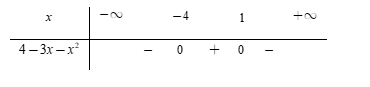
Dựa vào bảng xét dấu, ta thấy \(4 - 3x - {x^2} > 0 \Leftrightarrow x \in \left( { - \,4;\,1} \right).\)

Vậy tập xác định của hàm số là \(D = \left( { - \,4;1} \right).\)

Hàm số xác định khi và chỉ khi \(\left\{ \begin{array}{l}{x^2} + x - 6 \ge 0\\x + 4 > 0\end{array} \right..\)

Phương trình \({x^2} + x - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x =  - \,3\end{array} \right.\) và \(x + 4 = 0 \Leftrightarrow x =  - \,4.\)

Bảng xét dấu

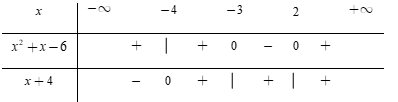
Dựa vào bảng xét dấu, ta thấy $\left\{ \begin{array}{l}{x^2} + x - 6 \ge 0\\x + 4 > 0\end{array} \right. \Leftrightarrow x \in \left( { - \,4; - \,3} \right] \cup \left[ {2;\, + \infty } \right).$

Vậy tập xác định của hàm số là $D = \left( { - \,4;\, - 3} \right] \cup \left[ {2;\, + \infty } \right).$

Yêu cầu bài toán $ \Leftrightarrow \left\{ \begin{array}{l}a = m - 1 \ne 0\\{\Delta _x} = {\left( {3m - 2} \right)^2} - 4\left( {m - 1} \right)\left( {3 - 2m} \right) > 0\end{array} \right.$

$ \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\9{m^2} - 12m + 4 - 4\left( { - 2{m^2} + 5m - 3} \right) > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\17{m^2} - 32m + 16 > 0\end{array} \right.\,\,\,\left(  *  \right)$

Ta có $\left\{ \begin{array}{l}a = 17 > 0\\{{\Delta '}_m} = {16^2} - 17.16 =  - \,16 < 0\end{array} \right.$ suy ra $17{m^2} - 32m + 16 > 0,{\rm{ }}\forall m \in \mathbb{R}.$

Do đó, hệ bất phương trình $\left(  *  \right) \Leftrightarrow m \ne 1$.

Hàm số \(y = \dfrac{{\sqrt {{x^2} + mx - m} }}{{{x^2} - 2mx + m + 2}}\) có tập xác định là \(\mathbb{R}\) khi và chỉ khi:

\(\left\{ \begin{array}{l}{x^2} + mx - m \ge 0,\forall x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\{x^2} - 2mx + m + 2 \ne 0,\forall x\,\,\,\,\,(2)\end{array} \right.\)

\(\left( 1 \right) \Leftrightarrow {\Delta _1} = {m^2} + 4m \le 0 \Leftrightarrow m\left( {m + 4} \right) \le 0 \Leftrightarrow  - 4 \le m \le 0.\)

\(\left( 2 \right) \Leftrightarrow {\Delta _2}' = {m^2} - m - 2 < 0\) \( \Leftrightarrow \left( {m + 1} \right)\left( {m - 2} \right) < 0 \Leftrightarrow  - 1 < m < 2.\)

Vậy \( - 1 < m \le 0.\)

Yêu cầu bài toán $ \Leftrightarrow \left\{ \begin{array}{l}a = m - 1 \ne 0\\{{\Delta '}_x} = {\left( { - \,1} \right)^2} - \left( {m - 1} \right)\left( {m + 1} \right) > 0\end{array} \right.$

$ \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\1 - {m^2} + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\{m^2} < 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\ - \,\sqrt 2  < m < \sqrt 2 \end{array} \right. \Leftrightarrow m \in \left( { - \,\sqrt 2 ;\sqrt 2 } \right)\backslash \left\{ 1 \right\}.$

Vậy phương trình có hai nghiệm phân biệt $ \Leftrightarrow m \in \left( { - \,\sqrt 2 ;\sqrt 2 } \right)\backslash \left\{ 1 \right\}.$

Tập nghiệm của \(2 - x \ge 0\) là \({S_1} = \left( { - \infty ;2} \right].\)

Xét dấu tam thức $f\left( x \right) = {x^2} - 4x + 3$  ta được:

Tập nghiệm của \({x^2} - 4x + 3 < 0\) là \({S_1} = \left( {1;3} \right).\)

Vậy tập nghiệm của hệ là \(S = {S_1} \cap {S_2} = \left( {1;2} \right].\)