Câu hỏi:
3 năm trước
Tìm tập hợp tất cả các giá trị của m để bất phương trình \({x^2} - 2x - m \le 0\) nghiệm đúng với mọi \(x \in \left[ {0;3} \right]\).
Trả lời bởi giáo viên
Đáp án đúng: b
\({x^2} - 2x - m \le 0 \Leftrightarrow {x^2} - 2x \le m\)
Xét \(f\left( t \right) = {x^2} - 2x\) trên đoạn \(\left[ {0;3} \right]\), ta có bảng biến thiên
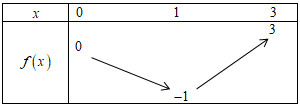
Vậy để bất phương trình \(f\left( t \right) = {x^2} - 2x \le m\) nghiệm đúng với mọi \(x \in \left[ {0;3} \right]\)
\( \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ {0;\,\,3} \right]} f\left( x \right) \Leftrightarrow m \ge 3\)
Hướng dẫn giải:
Cô lập m, lập bảng biến thiên khảo sát từ đó suy ra m

