Trả lời bởi giáo viên
Đáp án đúng: d
Hàm số y=x+√x2+4x−5
ĐKXĐ: x2+4x−5≥0
⇔(x−1)(x+5)≥0 ⇔[x≤−5x≥1
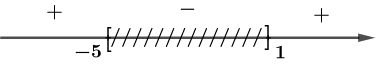
Vậy tập xác định của hàm số y=x+√x2+4x−5 là D=(−∞;−5]∪[1;+∞).
Hướng dẫn giải:
f(x)=2n√P(x)⇒KX:P(x)≥0

