Khẳng định nào sau đây là đúng khi nói về “góc lượng giác”?
Góc hình học \(\widehat {AOB}\) điểm đầu \(A\), điểm cuối \(B\) trên đường tròn định hướng là một góc lượng giác.
Cho góc lượng giác \(\left( {Ox,Oy} \right) = {22^0}30' + k{360^0}.\) Với giá trị \(k\) bằng bao nhiêu thì góc \(\left( {Ox,Oy} \right) = {1822^0}30'\)?
Ta có:
\(\begin{array}{l}\left( {Ox,Oy} \right) = {1822^0}30'\\ \Leftrightarrow {22^0}30' + k{.360^0} = {1822^0}30'\\ \Leftrightarrow k = 5\end{array}\)
Cho góc lượng giác \(\alpha = \dfrac{\pi }{2} + k2\pi \). Tìm $k$ để $10\pi < \alpha < 11\pi .$
Ta có
$\begin{array}{l}10\pi < \alpha < 11\pi \Leftrightarrow 10\pi < \dfrac{\pi }{2} + k2\pi < 11\pi \\ \Leftrightarrow \dfrac{{19\pi }}{2} < k2\pi < \dfrac{{21\pi }}{2} \Leftrightarrow k = 5\end{array}$
Một chiếc đồng hồ, có kim chỉ giờ \(OG\) chỉ số \(9\) và kim phút \(OP\) chỉ số$12$ . Số đo của góc lượng giác \(\left( {OG,OP} \right)\) là
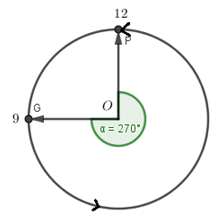
Quan sát hình vẽ ta thấy góc \(\left( {OG,OP} \right)\) có tia đầu \(OG\) và tia cuối \(OP\), chiều dương ngược chiều kim đồng hồ nên \(\left( {OG,OP} \right) = {270^0} + k{360^0}\) hoặc nếu theo chiều âm các em có thể kết luận \(\left( {OG,OP} \right) = - {90^0} + k{360^0}\)
Trên đường tròn lượng giác có điểm gốc là \(A\). Điểm \(M\)thuộc đường tròn sao cho cung lượng giác \(AM\) có số đo \({45^0}\). Gọi \(N\) là điểm đối xứng với \(M\) qua trục \(Ox\), số đo cung lượng giác \(AN\) bằng
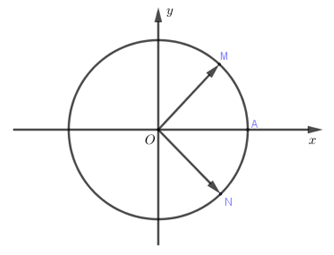
Vì số đo cung \(AM\) bằng \({45^0}\) nên \(\widehat {AOM} = {45^0}\), \(N\) là điểm đối xứng với \(M\) qua trục \(Ox\) nên $\widehat {AON} = {45^0}$.
Do đó \(\left( {OA,ON} \right) = - {45^0} + k{360^0}\) nên số đo cung lượng giác \(AN\) là \( - \,\,{45^o} + k{360^o},\,\,k \in \mathbb{Z}\).
Trên đường tròn với điểm gốc là \(A\). Điểm \(M\) thuộc đường tròn sao cho cung lượng giác $AM$ có số đo \({60^0}\). Gọi \(N\) là điểm đối xứng với điểm \(M\) qua trục \(Oy\), số đo cung lượng giác \(AN\) là:
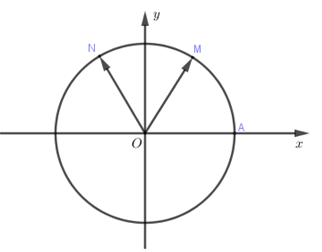
Ta có \(\widehat {AOM} = {60^0}\), \(\widehat {MON} = {60^0}\)
Nên \(\widehat {AON} = {120^0}\).
Khi đó số đo cung lượng giác \(AN\) bằng \({120^0} + k{360^0}\).
Trên đường tròn lượng giác với điểm gốc là \(A\). Điểm \(M\) thuộc đường tròn sao cho cung lượng giác \(AM\) có số đo \({75^0}\). Gọi \(N\) là điểm đối xứng với điểm \(M\) qua gốc tọa độ \(O\), số đo cung lượng giác \(AN\) bằng:
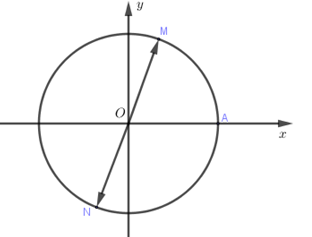
Ta có \(\widehat {AOM} = {75^0}\), \(\widehat {MON} = {180^0} \Rightarrow \widehat {AON} = {105^0}\)
Do đó, cung lượng giác \(AN\) có số đo bằng \( - {105^0} + k{360^0},\,\,\,k \in \mathbb{Z}\).
Cho bốn cung lượng giác (trên một đường tròn định hướng): $\alpha = - \dfrac{{5\pi }}{6},$ $\beta = \dfrac{\pi }{{\rm{3}}}$, $\gamma = \dfrac{{{\rm{25}}\pi }}{{\rm{3}}},$ $\delta = \dfrac{{{\rm{19}}\pi }}{{\rm{6}}}$ có cùng điểm đầu. Các cung nào có điểm cuối trùng nhau:
Cách 1. Ta có \(\delta - \alpha = 4\pi \,\, \Rightarrow \) hai cung \(\alpha \) và \(\delta \) có điểm cuối trùng nhau.
Và \(\gamma - \beta = 8\pi \,\, \Rightarrow \) hai cung \(\beta \) và \(\gamma \) có điểm cuối trùng nhau.
Các cặp góc lượng giác sau ở trên cùng một đường tròn đơn vị, cùng tia đầu và tia cuối. Hãy nêu kết quả SAI trong các kết quả sau đây:
Cặp góc lượng giác \(a\) và \(b\) ở trên cùng một đường tròn đơn vị, cùng tia đầu và tia cuối.
Khi đó \(a = b + k2\pi \), \(k \in \mathbb{Z}\) hay \(k = \dfrac{{a - b}}{{2\pi }}\).
Dễ thấy, ở đáp án B vì \(k = \dfrac{{\dfrac{\pi }{{10}} - \dfrac{{152\pi }}{5}}}{{2\pi }} = - \dfrac{{303}}{{20}} \notin \mathbb{Z}\).
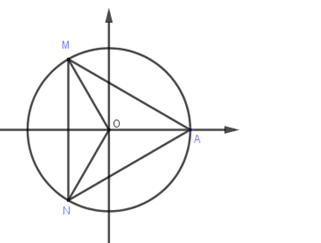
Trên đường tròn lượng giác gốc \(A\), cung lượng giác nào có các điểm biểu diễn tạo thành tam giác đều ?
Đáp án A : Cung lượng giác có số đo \(\dfrac{{k2\pi }}{3}\).
- Với \(k = 1 \Rightarrow \dfrac{{1.2\pi }}{3} = \dfrac{{2\pi }}{3}\) ta có điểm \(M\).
- Với \(k = 2 \Rightarrow \dfrac{{k2\pi }}{3} = \dfrac{{4\pi }}{3}\) ta có điểm \(N\).
- Với \(k = 3 \Rightarrow \dfrac{{k2\pi }}{3} = 2\pi \) ta có điểm \(A\).
- Với \(k = 4 \Rightarrow \dfrac{{k2\pi }}{3} = \dfrac{{8\pi }}{3} = 2\pi + \dfrac{{2\pi }}{3}\) có điểm biểu diễn \(M\).
Tương tự với các giá trị khác của \(k\) ta cũng chie thu được \(3\) điểm \(M,N,A\) trên đường tròn lượng giác và ba điểm đó tạo thành một tam giác đều nên A thỏa mãn.
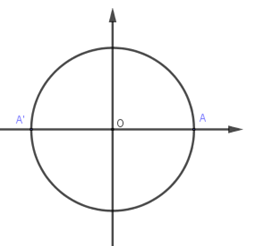
Đáp án B : Chỉ có hai điểm biểu diễn là \(A\) và \(A'\) nên loại B.
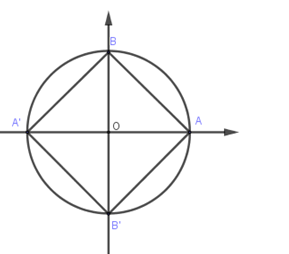
Đáp án C : Có \(4\) điểm biểu diễn \(A,A',B,B'\) tạo thành hình vuông nên loại C.
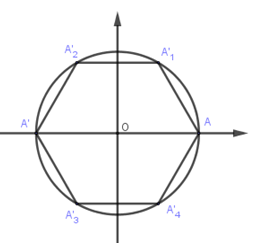
Đáp án D : Có \(6\) điểm biểu diễn tạo thành hình lục giác đều nên loại D.
Trên đường tròn lượng giác gốc \(A\), cung lượng giác nào có các điểm biểu diễn tạo thành hình vuông
Ta thấy: \(k2\pi :\dfrac{{k\pi }}{2} = 4\) nên có \(4\) điểm biểu diễn cho cung lượng giác đó, đáp án A thỏa mãn.
Ngoài ra: \(k2\pi :k\pi = 2\) nên có \(2\) điểm biểu diễn cho cung lượng giác đó, đáp án B loại.
\(k2\pi :\dfrac{{k2\pi }}{3} = 3\) nên có \(3\) điểm biểu diễn và chúng là thành một tam giác đều.
\(k2\pi :\dfrac{{k\pi }}{3} = 6\) nên có \(6\) điểm biểu diễn và chúng làm thành một lục giác đều.
\(M\) là điểm biểu diễn của cung lượng giác \(\alpha = - {15^0}.\)
\( \Rightarrow \) Số đo cung lượng giác biểu diễn bởi điểm \(M\) \( = - {15^o} + k{.360^o}\,\,\,\,\,\,\,(k \in \mathbb{Z})\)
Dễ thấy để cung có số đo dương nhỏ nhất \( \Leftrightarrow k = 1\)
Khi đó số đo cung là \( - {15^o} + {360^o} = {345^o}\)
Trên đường tròn lượng giác, cho điểm M với \(AM = 1\) như hình vẽ dưới đây.
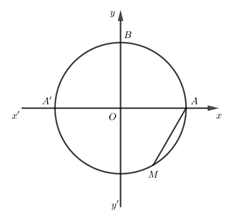
Số đo cung AM là:
Dễ thấy \(OA = OM = AM = 1 \Rightarrow \Delta OAM\) đều \( \Rightarrow \angle AOM = {60^o} = \dfrac{\pi }{3}\)
Vì M nằm dưới trục hoành \( \Rightarrow \) Số đo cung AM \( = - \dfrac{\pi }{3} + k2\pi ,\,\,\,\,k \in \mathbb{Z}\)

