Dấu của nhị thức bậc nhất

Đặt $f\left( x \right) = \left( {2 - x} \right)\left( {x + 1} \right)\left( {3 - x} \right)$

Phương trình $2 - x = 0 \Leftrightarrow x = 2;\,\,\,x + 1 = 0 \Leftrightarrow x =  - \,1$ và $3 - x = 0 \Leftrightarrow x = 3.$

Ta có bảng xét dấu

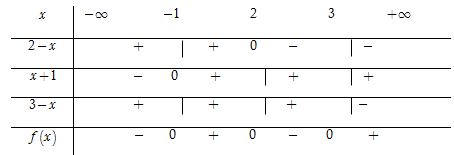
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \,\infty ; - \,1} \right] \cup \left[ {2;3} \right].$

Vậy bất phương trình đã cho có $2$ nghiệm nguyên dương.

Đặt $f\left( x \right) = x\left( {x - 2} \right)\left( {x + 1} \right).$

Phương trình $x = 0;\,\,x - 2 = 0 \Leftrightarrow x = 2$ và $x + 1 = 0 \Leftrightarrow x =  - \,1.$ Ta có bảng xét dấu

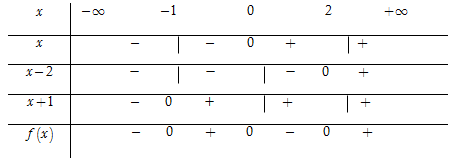
Dựa vào bảng xét dấu, ta thấy $f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \,1;0} \right) \cup \left( {2; + \,\infty } \right).$

Vậy nghiệm nguyên nhỏ nhất thỏa mãn bất phương trình là $3.$

Đặt $f\left( x \right) = \dfrac{{2 - x}}{{2x + 1}}.$ Ta có $2 - x = 0 \Leftrightarrow x = 2$ và $2x + 1 = 0 \Leftrightarrow x =  - \dfrac{1}{2}.$

Bảng xét dấu

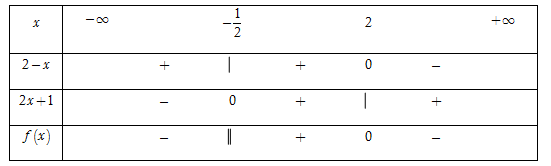
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \ge 0 \Leftrightarrow  - \dfrac{1}{2} < x \le 2.$

Vậy tập nghiệm của bất phương trình là $S = \left( { - \dfrac{1}{2};2} \right].$

\(\dfrac{{2x - 4}}{{3 - x}} \ge 0\)     

ĐKXĐ: \(x \ne 3\)   

Đặt \(f\left( x \right) = \dfrac{{2x - 4}}{{3 - x}}\) . Ta có bảng:

Vậy \(f\left( x \right) \ge 0 \Leftrightarrow 2 \le x < 3 \Rightarrow \) Tập nghiệm của phương trình là \(\left[ {2;3} \right).\)

Bất phương trình $\dfrac{3}{{1 - x}} \ge \dfrac{5}{{2x + 1}} \Leftrightarrow \dfrac{{11x - 2}}{{\left( {1 - x} \right)\left( {2x + 1} \right)}} \ge 0.$

Đặt $f\left( x \right) = \dfrac{{11x - 2}}{{\left( {1 - x} \right)\left( {2x + 1} \right)}}.$

Ta có $11x - 2 = 0 \Leftrightarrow x = \dfrac{2}{{11}};\,\,$$1 - x = 0 \Leftrightarrow x = 1,$$2x + 1 = 0 \Leftrightarrow x =  - \dfrac{1}{2}$.

Bảng xét dấu

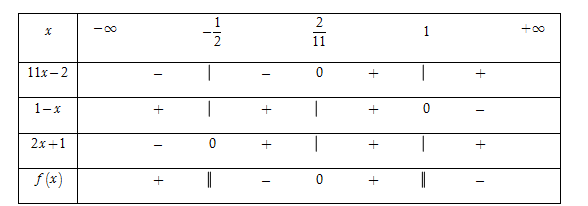
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x <  - \dfrac{1}{2}\\\dfrac{2}{{11}} \le x < 1\end{array} \right..$

Vậy tập nghiệm của bất phương trình là $S = \left( { - \infty ; - \dfrac{1}{2}} \right) \cup \left[ {\dfrac{2}{{11}};1} \right).$

Bất phương trình \(\dfrac{{2x}}{{x + 1}} - \dfrac{1}{{x - 1}} \le 2 \Leftrightarrow \dfrac{{1 - 3x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} \le 0.\)

Đặt $f\left( x \right) = \dfrac{{1 - 3x}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}.$

Ta có $1 - 3x = 0 \Leftrightarrow x = \dfrac{1}{3};$$x - 1 = 0 \Leftrightarrow x = 1;$ $x + 1 = 0 \Leftrightarrow x =  - 1$.

Bảng xét dấu

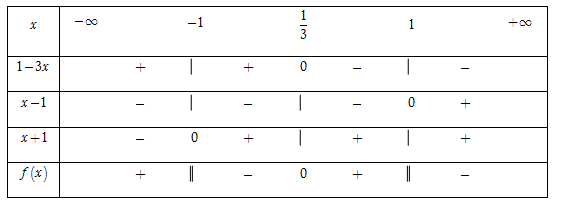
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \le 0 \Leftrightarrow \left[ \begin{array}{l} - \,1 < x \le \dfrac{1}{3}\\x > 1\end{array} \right..$

Vậy tập nghiệm của bất phương trình là $S = \left( { - \,1;\dfrac{1}{3}} \right] \cup \left( {1; + \,\infty } \right).$

Bất phương trình $\dfrac{1}{x} + \dfrac{2}{{x + 4}} < \dfrac{3}{{x + 3}} \Leftrightarrow \dfrac{{x + 12}}{{x\left( {x + 3} \right)\left( {x + 4} \right)}} < 0.$

Đặt $f\left( x \right) = \dfrac{{x + 12}}{{x\left( {x + 3} \right)\left( {x + 4} \right)}}.$

Ta có $x + 12 = 0 \Leftrightarrow x =  - 12;$$x + 3 = 0 \Leftrightarrow x =  - 3;$ $x + 4 = 0 \Leftrightarrow x =  - 4$.

Bảng xét dấu

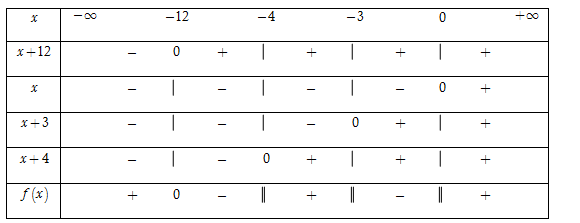
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l} - \,12 < x <  - \,4\\ - \,3 < x < 0\end{array} \right..$

Vậy tập nghiệm của bất phương trình là $S = \left( { - \,12; - \,4} \right) \cup \left( { - \,3;0} \right).$

Ta có $\left| {x - 1} \right| < 1 \Leftrightarrow  - \,1 < x - 1 < 1 \Leftrightarrow 0 < x < 2.$

Ta có $\left| {3x - 4} \right| \le 2 \Leftrightarrow  - \,2 \le 3x - 4 \ge 2$ $ \Leftrightarrow 2 \le 3x \le 6 \Leftrightarrow \dfrac{2}{3} \le x \le 2$.

Ta có $\left| {1 - 3x} \right| > 2$ $ \Leftrightarrow \left[ \begin{array}{l}1 - 3x > 2\\1 - 3x <  - 2\end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} - 1 > 3x\\3x > 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x <  - \dfrac{1}{3}\\x > 1\end{array} \right.$

Vậy tập nghiệm của bất phương trình đã cho là $S = \left( { - \,\infty ; - \dfrac{1}{3}} \right) \cup \left( {1; + \,\infty } \right).$

Điều kiện: $x + 1 \ne 0 \Leftrightarrow x \ne  - \,1.$

Bất phương trình $\left| {\dfrac{{2 - x}}{{x + 1}}} \right| \ge 2 \Leftrightarrow \left[ \begin{array}{l}\dfrac{{2 - x}}{{x + 1}} \ge 2\\\dfrac{{2 - x}}{{x + 1}} \le  - 2\end{array} \right.$$ \Leftrightarrow \left[ \begin{array}{l}\dfrac{{2 - x}}{{x + 1}} - 2 \ge 0\\\dfrac{{2 - x}}{{x + 1}} + 2 \le 0\end{array} \right.$

\( \Leftrightarrow \left[ \begin{array}{l}
\dfrac{{2 - x - 2x - 2}}{{x + 1}} \ge 0\\
\dfrac{{2 - x + 2x + 2}}{{x + 1}} \le 0
\end{array} \right. \) \(\Leftrightarrow \left[ \begin{array}{l}
\dfrac{{ - 3x}}{{x + 1}} \ge 0\\
\dfrac{{x + 4}}{{x + 1}} \le 0
\end{array} \right. \) \(\Leftrightarrow \left[ \begin{array}{l}
\dfrac{x}{{x + 1}} \le 0\,\,\left( 1 \right)\\
\dfrac{{x + 4}}{{x + 1}} \le 0\,\,\left( 2 \right)
\end{array} \right.\)

Giải $\left( 1 \right),$ ta có bảng xét dấu:

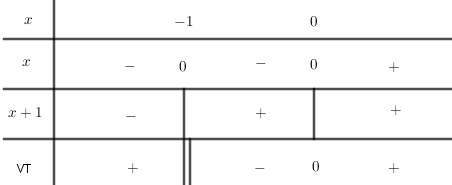
Ta có bất phương trình $\left( 1 \right) \Leftrightarrow \dfrac{x}{{x + 1}} \le 0 \Leftrightarrow  - \,1 < x \le 0.$

Giải $\left( 2 \right),$ ta có bảng xét dấu:

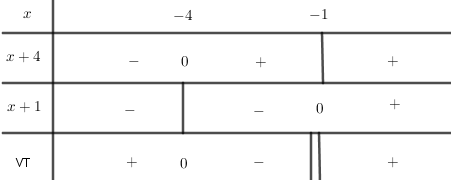
Ta có bất phương trình $\left( 2 \right) \Leftrightarrow  - \,4 \le x <  - \,1.$

Do đó, tập nghiệm của bất phương trình là $S = \left[ { - \,4; - \,1} \right) \cup \left( { - \,1;0} \right].$

Vậy có tất cả $4$ giá trị nguyên $x$ cần tìm là $x = \left\{ { - \,4; - \,3; - \,2;0} \right\}.$

Bất phương trình \(1 \le \left| {x - 2} \right| \le 4 \Leftrightarrow \left\{ \begin{array}{l}\left| {x - 2} \right| \le 4\\\left| {x - 2} \right| \ge 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - \,4 \le x - 2 \le 4\\\left[ \begin{array}{l}x - 2 \ge 1\\x - 2 \le  - \,1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - \,2 \le x \le 6\\\left[ \begin{array}{l}x \ge 3\\x \le 1\end{array} \right.\end{array} \right.\)

Do đó, tập nghiệm của bất phương trình là $S = \left[ { - \,2;1} \right] \cup \left[ {3;6} \right].$

Vậy số nghiệm nguyên thỏa mãn bất phương trình là $8.$

Ta có $\left| {x - 3} \right| > \left| {2x + 4} \right| \Leftrightarrow {\left| {x - 3} \right|^2} > {\left| {2x + 4} \right|^2} \Leftrightarrow {\left( {x - 3} \right)^2} - {\left( {2x + 4} \right)^2} > 0$

$ \Leftrightarrow \left( {x - 3 - 2x - 4} \right)\left( {x - 3 + 2x + 4} \right) > 0 \Leftrightarrow \left( { - \,x - 7} \right)\left( {3x + 1} \right) > 0 \Leftrightarrow  - \,7 < x <  - \dfrac{1}{3}.$

Vậy tập nghiệm của bất phương trình là $S = \left( { - \,7; - \dfrac{1}{3}} \right).$

TH1. Với $2x - 4 \ge 0 \Leftrightarrow x \ge 2,$ ta có $x + 12 \ge \left| {2x - 4} \right| \Leftrightarrow x + 12 \ge 2x - 4 \Leftrightarrow x \le 16.$

Kết hợp với điều kiện $x \ge 2,$ ta được tập nghiệm ${S_1} = \left[ {2;16} \right].$

TH2. Với $2x - 4 < 0 \Leftrightarrow x < 2,$ ta có $x + 12 \ge  - \,2x + 4 \Leftrightarrow 3x \ge  - \,8 \Leftrightarrow x \ge  - \dfrac{8}{3}.$

Kết hợp với điều kiện $x < 2,$ ta được tập nghiệm ${S_2} = \left[ { - \dfrac{8}{3};2} \right).$

Do đó, tập nghiệm của bất phương trình là $S = {S_1} \cup {S_2} = \left[ { - \dfrac{8}{3};16} \right].$

Vậy số nghiệm nguyên $x$ thỏa mãn bất phương trình là $19.$

Ta có $\left| {3x - 4} \right| \ge x - 3$$ \Leftrightarrow \left[ \begin{array}{l}3x - 4 \ge x - 3\\3x - 4 \le  - \left( {x - 3} \right)\end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l}2x \ge 1\\4x \le 7\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge \dfrac{1}{2}\\x \le \dfrac{7}{4}\end{array} \right.$

Biểu diễn trên trục số:

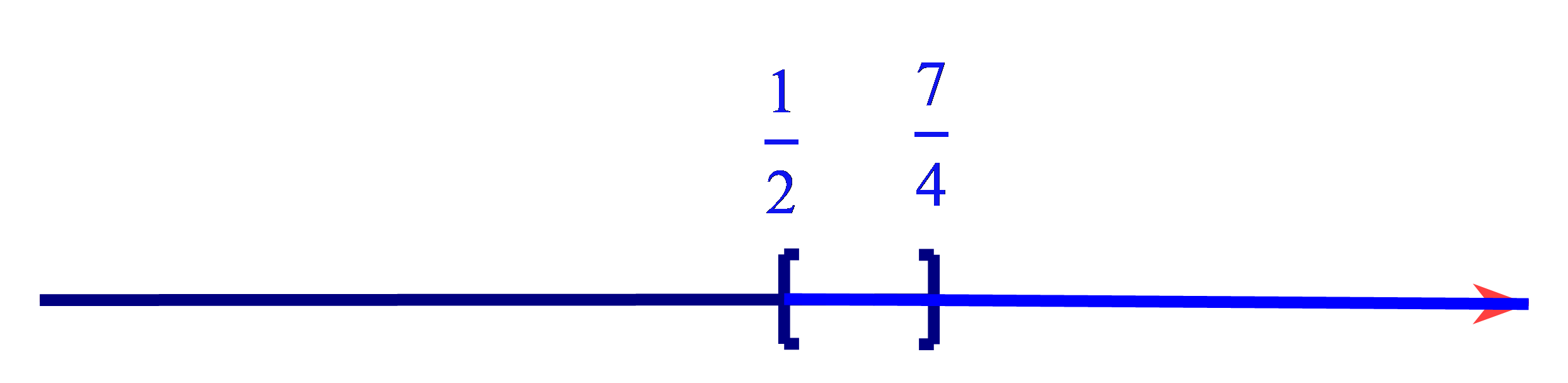
Suy ra \(x\in R\).

Vậy tập nghiệm của bất phương trình là $S =R.$

Xét bất phương trình $\left| {x + 1} \right| - \left| {x - 2} \right| \ge 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left(  *  \right).$

Bảng xét dấu

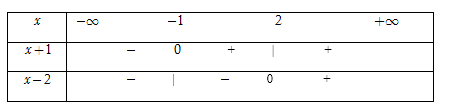
TH1. Với $x <  - \,1,$ khi đó $\left(  *  \right) \Leftrightarrow  - \,x - 1 + x - 2 \ge 3 \Leftrightarrow  - \,3 \ge 3$ (vô lý) suy ra ${S_1} = \emptyset .$

TH2. Với $ - \,1 \le x < 2,$ khi đó $\left(  *  \right) \Leftrightarrow x + 1 + x - 2 \ge 3 \Leftrightarrow 2x \ge 4 \Leftrightarrow x \ge 2.$

Kết hợp với điều kiện $ - \,1 \le x < 2,$ ta được tập nghiệm ${S_2} = \emptyset .$

TH3. Với $x \ge 2,$ khi đó $\left(  *  \right) \Leftrightarrow x + 1 - x + 2 \ge 3 \Leftrightarrow 3 \ge 3$ (luôn đúng).

Kết hợp với điều kiện $x \ge 2,$ ta được tập nghiệm ${S_3} = \left[ {2; + \,\infty } \right).$

Vậy tập nghiệm của bất phương trình là $S = {S_1} \cup {S_2} \cup {S_3} = \left[ {2; + \,\infty } \right).$

Điều kiện: $x \ne 0.$

TH1. Với $x + 2 \ge 0 \Leftrightarrow x \ge  - \,2,$ ta có

$\dfrac{{\left| {x + 2} \right| - x}}{x} \le 2 \Leftrightarrow \dfrac{{x + 2 - x}}{x} \le 2$

\( \Leftrightarrow \frac{2}{x} - 2 \le 0 \Leftrightarrow \frac{{2 - 2x}}{x} \le 0\) \( \Leftrightarrow \frac{{2\left( {1 - x} \right)}}{x} \le 0\)

$ \Leftrightarrow \dfrac{{1 - x}}{x} \le 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x < 0\end{array} \right.$

Kết hợp với điều kiện $x \ge  - \,2,$ ta được tập nghiệm ${S_1} = \left[ { - \,2;0} \right) \cup \left[ {1; + \,\infty } \right).$

TH2. Với $x + 2 < 0 \Leftrightarrow x <  - \,2,$ ta có $\dfrac{{\left| {x + 2} \right| - x}}{x} \le 2 \Leftrightarrow \dfrac{{ - x - 2 - x}}{x} \le 2$$ \Leftrightarrow  - \dfrac{{2x + 2}}{x} \le 2$

$ \Leftrightarrow  - \dfrac{{x + 1}}{x} \le 1 \Leftrightarrow 1 + \dfrac{{x + 1}}{x} \ge 0$ $ \Leftrightarrow \dfrac{{2x + 1}}{x} \ge 0 \Leftrightarrow \left[ \begin{array}{l}x > 0\\x \le  - \dfrac{1}{2}\end{array} \right.$

Kết hợp với điều kiện $x <  - \,2,$ ta được tập nghiệm là ${S_2} = \left( { - \,\infty ; - 2} \right).$

Vậy tập nghiệm của bất phương trình là $S = {S_1} \cup {S_2} $ \( = \left[ { - 2;0} \right) \cup \left[ {1; + \infty } \right) \cup \left( { - \infty ; - 2} \right)\) $= \left( { - \,\infty ;0} \right) \cup \left[ {1; + \,\infty } \right).$

Ta có \(f\left( x \right) = 0 \Leftrightarrow \left( {x + 5} \right)\left( {3 - x} \right) = 0.\)

Phương trình \(x + 5 = 0 \Leftrightarrow x =  - \,5\) và \(3 - x = 0 \Leftrightarrow x = 3.\)

Bảng xét dấu:

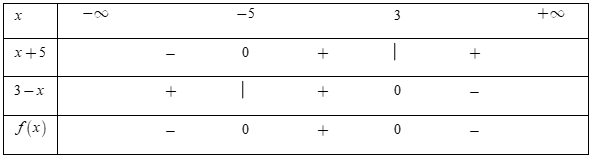
Dựa vào bảng xét dấu, ta thấy rằng \(f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \,\infty ; - \,5} \right] \cup \left[ {3; + \,\infty } \right).\)

Ta có $f\left( x \right) \le 0 \Leftrightarrow \dfrac{1}{{3x - 6}} \le 0 \Leftrightarrow 3x - 6 < 0 \Leftrightarrow x < 2 \Leftrightarrow x \in \left( { - \,\infty ;2} \right).$

- Phương trình $x + 3 = 0 \Leftrightarrow x =  - \,3;\,\,2 - x = 0 \Leftrightarrow x = 2$ và $x - 1 = 0 \Leftrightarrow x = 1.$

- Bảng xét dấu

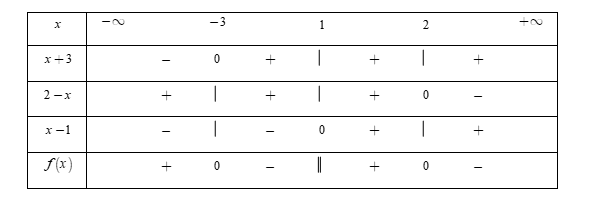
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \,\infty ; - \,3} \right) \cup \left( {1;2} \right).$