Với \(\overrightarrow {DE} \) (khác vectơ - không) thì độ dài đoạn \(ED\) được gọi là
Véc tơ \(\overrightarrow {DE} \) và \(\overrightarrow {ED} \) đều có độ dài là đoạn thẳng \(DE\).
Cho \(3\) điểm phân biệt \(A\),\(B\),\(C\). Khi đó khẳng định nào sau đây đúng nhất ?
Ba điểm \(A\),\(B\),\(C\) thẳng hàng khi và chỉ khi hai trong các véc tơ tạo thành từ \(3\) điểm đó cùng phương.
Do đó cả ba đáp án A, B, C đều đúng.
Mệnh đề nào sau đây đúng ?
Ta có vectơ \(\overrightarrow 0 \) cùng hướng với mọi vectơ nên nó cùng phương với mọi véc tơ.
Khẳng định nào sau đây đúng ?
Hai vectơ cùng phương với 1 vectơ thứ ba khác $\mathop 0\limits^ \to $thì cùng phương.
Cho vectơ $\overrightarrow a $. Mệnh đề nào sau đây đúng ?
Cho vectơ \(\overrightarrow a \), có vô số vectơ \(\overrightarrow u \)cùng hướng và cùng độ dài với vectơ \(\overrightarrow a \). Nên có vô số vectơ $\overrightarrow u $ mà $\overrightarrow u = \overrightarrow a $.
Cho ba điểm $M,N,P$ thẳng hàng, trong đó điểm $N$ nằm giữa hai điểm $M$ và $P$. Khi đó các cặp vecto nào sau đây cùng hướng ?

Quan sát hình vẽ ta thấy: \(\overrightarrow {MN} \) và \(\overrightarrow {MP} \) là hai vectơ cùng hướng.
Cho hình vuông $ABCD$, khẳng định nào sau đây đúng:

Ta có \(ABCD\) là hình vuông. Suy ra $\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|$.
Cho tam giác đều $ABC$. Mệnh đề nào sau đây sai ?
Ta có tam giác đều \(ABC \Rightarrow \overrightarrow {AB} ,\overrightarrow {BC} \) không cùng hướng $ \Rightarrow \overrightarrow {AB} \ne \overrightarrow {BC} $
Do đó A sai, B đúng và C, D cũng đúng.
Cho $3$ điểm \(A\),\(B\),\(C\) phân biệt không thẳng hàng, $M$ là điểm bất kỳ. Mệnh đề nào sau đây đúng?
Bước 1:
Ta có $3$ điểm \(A\),\(B\),\(C\) không thẳng hàng, $M$ là điểm bất kỳ.
Trước hết ta chứng tỏ :$\overrightarrow {MA}\ne\overrightarrow {MB}$ \(\forall \) $M$ bằng phương pháp chứng minh phản chứng.
Giả sử \(\exists M:\)$\overrightarrow {MA} = \overrightarrow {MB}$.
Khi đó $\overrightarrow {MA}$ và $\overrightarrow {MB}$ cùng hướng và cùng độ dài.
Suy ra $M, A, B$ thẳng hàng, $MA = MB$ và $M$
=>$M$ vừa là trung điểm của $AB$
=>$\overrightarrow {MA} = \overrightarrow {BM}\ne \overrightarrow {MB}$ (vô lý)
Vậy $\overrightarrow {MA}\ne\overrightarrow {MB}$ \(\forall \) $M$.
Bước 2:
Do đó đáp án A sai.
Đáp án B sai vì: $\overrightarrow {MA}\ne\overrightarrow {MB}$ \(\forall \) $M$, tức là không thể tồn tại điểm $M$ thỏa mãn $\overrightarrow {MA}=\overrightarrow {MB}$ thì cũng không thể tồn tại M thỏa mãn $\overrightarrow {MA}=\overrightarrow {MB}=\overrightarrow {MC}$
Đáp án C đúng vì:
$\overrightarrow {MA}\ne\overrightarrow {MB}$ \(\forall \) $M$
Tương tự ta cũng có $\overrightarrow {MA}\ne\overrightarrow {MC}$ \(\forall \) $M$.
=> Mọi điểm $M$ ta đều có $\overrightarrow {MA} \ne \overrightarrow {MB}\ne \overrightarrow {MC}$
Đáp án D sai vì
$\overrightarrow {MA}\ne\overrightarrow {MB}$ với mọi $M$ rồi thì không thể tồn tại $M$ để $\overrightarrow {MA}=\overrightarrow {MB}$
Cho tam giác \(ABC\) có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh\(A\),\(B\), \(C\) ?
Ta có các vectơ đó là: $\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BA} ,\overrightarrow {BC} ,\overrightarrow {CA} ,\overrightarrow {CB} $.
Gọi $C$ là trung điểm của đoạn $AB$. Hãy chọn khẳng định đúng trong các khẳng định sau :
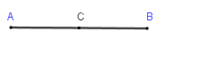
Ta có \(C\) là trung điểm của đoạn \(AB\) nên $\overrightarrow {AB} $ và $\overrightarrow {AC} $ cùng hướng.
Cho lục giác đều $ABCDEF$ tâm $O$. Ba vectơ bằng vecto \(\overrightarrow {BA} \) là:

Ba vectơ bằng vecto \(\overrightarrow {BA} \) là $\overrightarrow {OF} ,\overrightarrow {DE} ,\overrightarrow {CO} $.
Cho tứ giác $ABCD$. Gọi $M,N,P,Q$ lần lượt là trung điểm của $AB,BC,CD,DA$. Trong các khẳng định sau, hãy tìm khẳng định sai?

Ta có \(MN\) là đường trung bình của tam giác \(ABC\).
Suy ra\(MN = \dfrac{1}{2}AC\) hay $\left| {\overrightarrow {MN} } \right| = \dfrac{1}{2}\left| {\overrightarrow {AC} } \right|$
Cho lục giác đều $ABCDEF$ tâm $O$. Các vectơ đối của vectơ $\overrightarrow {OD} $ là:
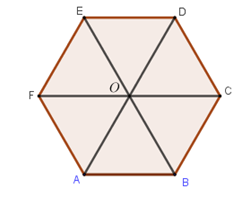
Các vectơ đối của vectơ $\overrightarrow {OD} $ là: $\overrightarrow {OA} ,\overrightarrow {DO} ,\overrightarrow {EF} ,\overrightarrow {CB}.$
Cho tam giác đều $ABC$ với đường cao $AH$. Đẳng thức nào sau đây đúng.

Đáp án A sai do hai vectơ ngược hướng.
Đáp án B đúng vì: \(ABC\) đều dẫn đến \(H\) là trung điểm \(BC\) và $\left| {\overrightarrow {AC} } \right|{\rm{ = }}\left| {\overrightarrow {BC} } \right| = 2\left| {\overrightarrow {HC} } \right|$ .
Đáp án C sai vì $\left| {\overrightarrow {AH} } \right| = \left| {\overrightarrow {HC} } \right|\tan {60^0} = \sqrt 3 \left| {\overrightarrow {HC} } \right|$
Đáp án D sai vì hai véc tơ \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương.
Cho hình bình hành $ABCD$. Đẳng thức nào sau đây sai.
Vì $ABCD$ là hình bình hành nên độ dài các cạnh đối bằng nhau, do đó các đáp án A, B, D đều đúng.
\(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BD} } \right|\) sai do \(ABCD\) là hình bình hành nên hai đường chéo chưa chắc bằng nhau.
Cho tam giác $ABC$ với trực tâm $H$. Gọi $D$ là điểm đối xứng với $B$ qua tâm $O$ của đường tròn ngoại tiếp tam giác $ABC$. Khẳng định nào sau đây là đúng ?
$\overrightarrow {HA} = \overrightarrow {CD} $ và $\overrightarrow {AD} = \overrightarrow {CH} $.
$\overrightarrow {HA} = \overrightarrow {CD} $ và $\overrightarrow {DA} = \overrightarrow {HC} $.

Ta có\(BD\) là đường kính$ \Rightarrow \overrightarrow {OB} = \overrightarrow {DO} $.
Ta có \(AH \bot BC,DC \bot BC \Rightarrow AH//DC(1)\)
Ta lại có\(CH \bot AB,DA \bot AB \Rightarrow CH//DA(2)\)
Từ \(\left( 1 \right)\left( 2 \right) \Rightarrow \)tứ giác \(HADC\) là hình bình hành\( \Rightarrow \overrightarrow {HA} = \overrightarrow {CD} ;\overrightarrow {AD} = \overrightarrow {HC} \).

