Cho tam giác \(ABC\) nội tiếp đường tròn tâm \(I\left( {2;\;1} \right)\), trọng tâm \(G\left( {\dfrac{7}{3};\;\dfrac{4}{3}} \right)\), phương trình đường thẳng \(AB:x - y + 1 = 0\). Giả sử điểm \(C\left( {{x_0};\;{y_0}} \right)\), tính \(2{x_0} + {y_0}\).
Trả lời bởi giáo viên
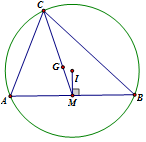
Gọi \(M\left( {a;\;a + 1} \right)\) là trung điểm \(AB\).
Ta có \(\overrightarrow {IM} = \left( {a - 2;\;a} \right)\), $1$ VTCP của $AB$ là \(\overrightarrow {{u_{AB}}} = \left( {1;\;1} \right)\).
Mà $\overrightarrow {IM} \bot \overrightarrow {{u_{AB}}} $ $ \Leftrightarrow \overrightarrow {IM} .\overrightarrow {{u_{AB}}} = 0$ \( \Leftrightarrow a - 2 + a = 0\) \( \Leftrightarrow a = 1\). Vậy \(M\left( {1;\;2} \right)\).
Nhận xét \(\overrightarrow {CG} = 2\overrightarrow {GM} \) \( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{7}{3} - {x_0} = 2\left( {1 - \dfrac{7}{3}} \right)\\\dfrac{4}{3} - {y_0} = 2\left( {2 - \dfrac{4}{3}} \right)\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 5\\{y_0} = 0\end{array} \right.\).
Vậy \(2{x_0} + {y_0} = 10\).
Hướng dẫn giải:
- Tìm tọa độ điểm \(M\) là trung điểm của \(AB\).
- Tìm tọa độ điểm \(C\) dựa vào tính chất trọng tâm.

