Câu hỏi:
2 năm trước
Một miếng giấy hình tam giác $ABC$ vuông tại \(A\) có diện tích $S$, gọi $I$ là trung điểm $BC$ và $O$ là trung điểm của $AI$. Cắt miếng giấy theo một đường thẳng qua $O$, đường thẳng này đi qua $M$, $N$ lần lượt trên các cạnh $AB$, $AC$. Khi đó diện tích miếng giấy chứa điểm$A$ có diện tích thuộc đoạn:
Trả lời bởi giáo viên
Đáp án đúng: a
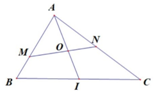
Đặt \(A\left( {0;\,0} \right)\), \(B\left( {4b;\,0} \right)\), \(C\left( {0;\,4c} \right)\) \( \Rightarrow \)\(I\left( {2b;2c} \right)\), \(O\left( {b,\,c} \right)\).
Đặt \(M\left( {t,\,0} \right)\) \( \Rightarrow \) \(N\left( {0,\,\dfrac{{ - ct}}{{b - t}}} \right)\).
Khi đó: \({S_{\Delta ABC}} = 8bc\), \({S_{\Delta AMN}} = \dfrac{{c{t^2}}}{{2\left( {t - b} \right)}} = \dfrac{c}{2}.f\left( t \right)\) với \(\dfrac{{4b}}{3} \le t \le 4b\).
Xét \(f\left( t \right) = \dfrac{{{t^2}}}{{t - b}}\) trong \(\left[ {\dfrac{{4b}}{3};4b} \right]\) ta có:
\(f\left( t \right) = \dfrac{{{t^2}}}{{t - b}}\)\( = t + b + \dfrac{{{b^2}}}{{t - b}}\)\( = t - b + \dfrac{{{b^2}}}{{t - b}} + 2b\) \( \ge 2\sqrt {\left( {t - b} \right).\dfrac{{{b^2}}}{{t - b}}} + 2b\) \( = 2b + 2b = 4b\)
Do đó \(f\left( t \right) \ge 4b,\forall t \in \left[ {\dfrac{{4b}}{3};4b} \right]\).
Dấu \('' = ''\) xảy ra khi \(t - b = \dfrac{{{b^2}}}{{t - b}} \Leftrightarrow t = 2b\).
Vậy \(\mathop {\min }\limits_{\left[ {\dfrac{{4b}}{3};4b} \right]} f\left( t \right) = 4b\) hay \(\min {S_{AMN}} = \dfrac{c}{2}.4b = 2bc\) khi \(t = 2b\).
\({f_{\max }} = \dfrac{{8bc}}{3}\) khi \(t = \dfrac{{4b}}{3} \vee t = 4b\)
\( \Rightarrow \)\(\dfrac{{{S_{ABC}}}}{4} \le {S_{AMN}} \le \dfrac{{{S_{ABC}}}}{3}\).
Hướng dẫn giải:
- Chọn hệ trục tọa độ có \(A\) làm gốc, tìm tọa độ các điểm còn lại theo hệ trục đã chọn.
- Tính diện tích tam giác \(ABC,AMN\) và đánh giá diện tích tam giác \(AMN\).
Câu hỏi khác
- Bài tập một số khái niệm phương trình đường thẳng toán 10 có lời giải
- Bài tập vị trí tương đối của đường thẳng với đường tròn toán 10 có lời giải
- Bài tập một số bài toán viết phương trình đường thẳng toán 10 có lời giải
- Bài tập phương trình đường tròn toán 10 có lời giải
- Bài tập khoảng cách và góc toán 10 có lời giải
