Trong mặt phẳng với hệ tọa độ \(Oxy\) cho hình chữ nhật \(ABCD\) biết \(AD = 2AB\), đường thẳng \(AC\) có phương trình \(x + 2y + 2 = 0\), \(D\left( {1;\,1} \right)\) và \(A\left( {a;\,b} \right)\,\,\,\,\,\,\left( {a,\,b \in \mathbb{R},\,a > 0} \right)\). Tính \(a + b\).

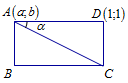
Cách 1: Gọi \(A\left( {a;b} \right)\). Vì \(A \in AC:x + 2y + 2 = 0\) nên \(a + 2b + 2 = 0 \Rightarrow a =  - 2b - 2\)

Do \(a > 0\) nên \( - 2b - 2 > 0 \Rightarrow b <  - 1\) \(\,\left( * \right)\)

Khi đó \(A\left( { - 2b - 2;b} \right)\). 

Ta có   \(\overrightarrow {AD}  = \left( {2b + 3;1 - b} \right)\) là véctơ chỉ phương của đường thẳng \(AD\).

            \(\vec u = \left( {2; - 1} \right)\) là véctơ chỉ phương của đường thẳng \(AC\).

Trên hình vẽ, \(\tan \alpha  = \dfrac{{DC}}{{AD}} = \dfrac{1}{2} \Rightarrow \cos \alpha  = \dfrac{2}{{\sqrt 5 }}\) \(\left( 1 \right)\)

Lại có \(\cos \alpha  = \dfrac{{\left| {\overrightarrow {AD} .\vec u} \right|}}{{\left| {\overrightarrow {AD} } \right|.\left| {.\vec u} \right|}} = \dfrac{{5\left| {b + 1} \right|}}{{\sqrt 5 \sqrt {{b^2} + 2b + 2} }}\) \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\dfrac{{5\left| {b + 1} \right|}}{{\sqrt 5 \sqrt {{b^2} + 2b + 2} }} = \dfrac{2}{{\sqrt 5 }} \Leftrightarrow {b^2} + 2b - 3 = 0 \Rightarrow b =  - 3\) (do \(\left( * \right)\)) \( \Rightarrow a = 4\).

Khi đó \(A\left( {4; - 3} \right)\), suy ra \(a + b = 1\). 

Cách 2: Gọi \(A\left( {a;b} \right)\). Vì \(A \in AC:x + 2y + 2 = 0\) nên \(a + 2b + 2 = 0 \Rightarrow a =  - 2b - 2\)

Do \(a > 0\) nên \( - 2b - 2 > 0 \Rightarrow b <  - 1\)\(\,\left( * \right)\), khi đó \(A\left( { - 2b - 2;b} \right)\). 

Vì \(C \in AC:x + 2y + 2 = 0\) nên \(C\left( { - 2c - 2;c} \right)\)

Ta có: \(\overrightarrow {AD}  = \left( {3 + 2b; - 1 - b} \right)\); \(\overrightarrow {CD}  = \left( {3 + 2c;1 - c} \right)\). 

Chọn \(\left\{ \begin{array}{l}\vec u \bot \overrightarrow {CD} \\\left| {\vec u} \right| = \left| {\overrightarrow {CD} } \right|\end{array} \right. \Rightarrow \vec u = \left( {c - 1;3 + 2c} \right)\)

Ta có: \(\left\{ \begin{array}{l}AD \bot CD\\AB = 2CD\end{array} \right. \Rightarrow \left[ \begin{array}{l}\overrightarrow {AD}  = 2\vec u\\\overrightarrow {AD}  =  - 2\vec u\end{array} \right.\)

*  Với \(\overrightarrow {AD}  = 2\vec u\) \( \Rightarrow \left\{ \begin{array}{l}3 + 2b = 2c - 2\\1 - b = 6 + 4c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 3\\c =  - \dfrac{1}{2}\end{array} \right.\)  (t/m)

*  Với \(\overrightarrow {AD}  =  - 2\vec u\) \( \Rightarrow \left\{ \begin{array}{l}3 + 2b =  - 2c + 2\\1 - b =  - 6 - 4c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 1\\c =  - \dfrac{3}{2}\end{array} \right.\)  (không t/m)

Vậy \(A\left( {4; - 3} \right)\), suy ra \(a + b = 1\).