Cho đường tròn \(\left( C \right):{x^2} + {y^2} + 6x - 2y + 5 = 0\) và điểm \(A\left( { - 4;2} \right)\). Đường thẳng \(d\) qua \(A\) cắt \(\left( C \right)\) tại \(2\) điểm \(M\), \(N\) sao cho \(A\) là trung điểm của \(MN\) có phương trình là
Trả lời bởi giáo viên
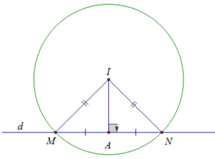
\(\left( C \right)\) có tâm \(I\left( { - 3;1} \right)\), bán kính \(R = \sqrt 5 \).
Đường thẳng qua \(A\left( { - 4;2} \right)\) có véc tơ pháp tuyến \(\overrightarrow {\,n\,} = \left( {a;b} \right)\) \(\left( {{a^2} + {b^2} \ne 0} \right)\) có phương trình dạng \(d:ax + by + 4a - 2b = 0\).
Tam giác \(IMN\) cân tại \(I\) có \(A\) là trung điểm \(MN\) nên $IA \bot MN$.
\( \Rightarrow d\left( {I;d} \right) = IA \Leftrightarrow \dfrac{{\left| {a - b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \sqrt 2 \Leftrightarrow {\left( {a - b} \right)^2} = 2\left( {{a^2} + {b^2}} \right) \Leftrightarrow a = - b\).
Chọn \(a = 1 \Rightarrow b = - 1\). Vậy phương trình đường thẳng \(d:x - y + 6 = 0\).
Hướng dẫn giải:
- Gọi phương trình đường thẳng có véc tơ pháp tuyến \(\left( {a;b} \right)\).
- Sử dụng điều kiện khoảng cách \(d\left( {I,d} \right) = IA\) để tìm mối quan hệ \(a,b\) suy ra phương trình đường thẳng.

