Trong mặt phẳng \(Oxy\), cho tam giác \(ABC\) có \(A\left( { - 4; - 1} \right)\), hai đường cao \(BH\) và \(CK\) có phương trình lần lượt là \(2x - y + 3 = 0\) và \(3x + 2y - 6 = 0\). Viết phương trình đường thẳng \(BC\) và tính diện tích tam giác \(ABC\).

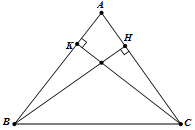
+ \(BH\) có véctơ pháp tuyến ${\overrightarrow n _{_{BH}}}\left( {2; - 1} \right)$. \(CK\) có véctơ pháp tuyến ${\overrightarrow n _{_{CK}}}\left( {3;2} \right)$.

+ Đường thẳng \(AB\) vuông góc \(CK\) nên nhận ${\overrightarrow n _{_{CK}}}\left( {3;2} \right)$ làm véctơ chỉ phương, vì thế \(AB\) có véctơ pháp tuyến ${\overrightarrow n _{_{AB}}}\left( {2; - 3} \right)$. Mặt khác \(AB\) đi qua \(A\left( { - 4; - 1} \right)\) nên có phương trình:

        \(2\left( {x + 4} \right) - 3\left( {y + 1} \right) = 0\) \( \Leftrightarrow 2x - 3y + 5 = 0\).

+ Đường thẳng \(AC\) vuông góc \(BH\) nên nhận ${\overrightarrow n _{_{BH}}}\left( {2; - 1} \right)$ làm véctơ chỉ phương, vì thế \(AC\) có véctơ pháp tuyến ${\overrightarrow n _{_{AC}}}\left( {1;2} \right)$. Mặt khác \(AC\) đi qua \(A\left( { - 4; - 1} \right)\) nên có phương trình:

        \(1\left( {x + 4} \right) + 2\left( {y + 1} \right) = 0\) \( \Leftrightarrow x + 2y + 6 = 0\).

+ \(B\) là giao điểm của \(AB\) và \(BH\). Xét hệ: \(\left\{ \begin{array}{l}2x - 3y + 5 = 0\\2x - y + 3 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = 1\end{array} \right.\) \( \Rightarrow B\left( { - 1;1} \right)\).

+ \(C\) là giao điểm của \(AC\) và \(CK\). Xét hệ: \(\left\{ \begin{array}{l}x + 2y + 6 = 0\\3x + 2y - 6 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y =  - 6\end{array} \right.\) \( \Rightarrow C\left( {6; - 6} \right)\).

+ Đường thẳng \(BC\) có véctơ chỉ phương là \(\overrightarrow {BC}  = \left( {7; - 7} \right)\) nên có véctơ pháp tuyến là \(\overrightarrow n  = \left( {7;7} \right)\). Vậy \(BC\) có phương trình: \(7\left( {x + 1} \right) + 7\left( {y - 1} \right) = 0\) \( \Leftrightarrow x + y = 0\).

+ \(BC = \sqrt {{7^2} + {{\left( { - 7} \right)}^2}}  = 7\sqrt 2 \).

+ Chiều cao kẻ từ \(A\) của tam giác \(ABC\) là \(d\left( {A,BC} \right) = \dfrac{{\left| { - 4 - 1} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{5}{{\sqrt 2 }}\).

+ Diện tích tam giác \(ABC\) là: \(S = \dfrac{1}{2}.7\sqrt 2 .\dfrac{5}{{\sqrt 2 }}\)\( = \dfrac{{35}}{2}\).